Question

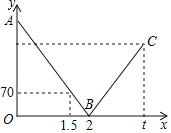
【题目】一辆快车从甲地驶往乙地，一辆慢车从乙地驶往甲地，两车同时出发，匀速行驶．设行驶的时间为x（时），两车之间的距离为y（千米），图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系．已知两车相遇时快车比慢车多行驶60千米．若快车从甲地到达乙地所需时间为t时，则此时慢车与甲地相距_____千米．

Answer 1

【答案】

【解析】

求出相遇前y与x的关系式，确定出甲乙两地的距离，进而求出两车的速度，即可求解．

设AB所在直线的解析式为：y＝kx+b，

把（1.5，70）与（2，0）代入得：

，

解得：，

∴AB所在直线的解析式为：y＝-140x+280，

令x＝0，得到y＝280，即甲乙两地相距280千米，

设两车相遇时，乙行驶了x千米，则甲行驶了（x+60）千米，

根据题意得：x+x+60＝280，

解得：x＝110，即两车相遇时，乙行驶了110千米，甲行驶了170千米，

∴甲车的速度为85千米/时，乙车速度为55千米/时，

根据题意得：280﹣55×（280÷85）＝（千米）．

则快车到达乙地时，慢车与甲地相距千米．

故答案为：