题目内容
【题目】二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,作直线
,作直线![]() ,将直线
,将直线![]() 下方的二次函数图象沿直线
下方的二次函数图象沿直线![]() 向上翻折,与其它剩余部分组成一个组合图象
向上翻折,与其它剩余部分组成一个组合图象![]() ,若线段
,若线段![]() 与组合图象
与组合图象![]() 有两个交点,则
有两个交点,则![]() 的取值范围为_____.
的取值范围为_____.
【答案】![]() 或
或![]()
【解析】
画出图形,采用数形结合,分类讨论讨论,分直线y=t在x轴上方和下方两种情况,需要注意的是,原抛物线与线段BC本来就有B、C两个交点.具体过程见详解.
解:分类讨论(一):原抛物线与线段BC就有两个交点B、C.
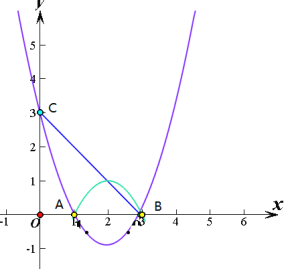
当抛物线在x轴下方部分,以x轴为对称轴向上翻折后,就会又多一个交点,所以要满足只有两个交点,直线y=t需向上平移,点B不再是交点,交点只有点C和点B、C之间的一个点,所以t >0;当以直线y=3为对称轴向上翻折时,线段![]() 与组合图象
与组合图象![]() 就只有点C一个交点了,不符合题意,所以t<3,故
就只有点C一个交点了,不符合题意,所以t<3,故![]() ;
;
(二)∵![]() =(x-2)2-1,
=(x-2)2-1,
∴抛物线沿![]() 翻折后的部分是抛物线
翻折后的部分是抛物线![]() )2+k在直线y=t的上方部分,当直线BC:y=-x+3与抛物线
)2+k在直线y=t的上方部分,当直线BC:y=-x+3与抛物线![]() 只有一个交点时,即
只有一个交点时,即![]() 的△=0,解得k=
的△=0,解得k=![]() ,此时线段BC与组合图象W的交点,既有C、B,又多一个,共三个,不符合题意,所以翻折部分需向下平移,即直线y=t向下平移,k=
,此时线段BC与组合图象W的交点,既有C、B,又多一个,共三个,不符合题意,所以翻折部分需向下平移,即直线y=t向下平移,k=![]() 时,抛物线
时,抛物线![]() )2+
)2+![]() 的顶点坐标为(2,
的顶点坐标为(2,![]() ),与
),与![]() 的顶点(2,-1)的中点是(2,-
的顶点(2,-1)的中点是(2,-![]() ),所以t<-
),所以t<-![]() ,又因为
,又因为![]() ,所以
,所以![]() .
.
综上所述:t的取值范围是:![]() 或
或![]()
故答案为:![]() 或
或![]() .
.

练习册系列答案
相关题目