Question

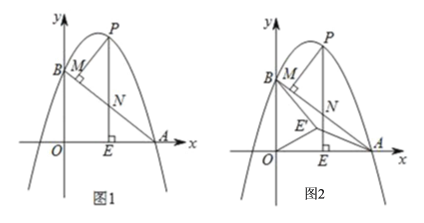
【题目】如图，在平面直角坐标系xOy中，直线l：y＝x+1交y轴于点A1，点A2，A3，…，An在直线l上，点B1，B2，B3，…，Bn在x轴的正半轴上，若△OA1B1，△A2B1B2，△A3B2B3，…，△AnBn﹣1Bn依次均为等腰直角三角形，则点B1的坐标是_____；点Bn的坐标是_____．

Answer 1

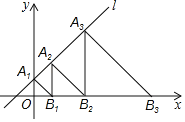
【答案】(1，0) (2n﹣1，0)

【解析】

首先求得点A与A1的坐标，由△OA1B1是等腰直角三角形可求得B1(1，0)，继而可得A2B1 =2，再由△A2B1B2是等腰直角三角形可求得B2(3，0)，B3(7，0)…，通过分析即可求得答案.

如图，y＝x+1与x轴交于点A(-1，0)，与y轴交点A1(0，1)，

则OA=OA1=1，

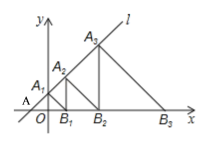
∵△OA1B1是等腰直角三角形，

∴OB1=OA1=1，

∴B1(1，0)，

∴当x=1时，y=x+1=2，

∴A2B1 =2，

∵△A2B1B2是等腰直角三角形，

∴B1B2=B1A2=2，

∴B2(3，0)，

同理B3(7，0)…，

∵B1的横坐标为1=21﹣1，

B2的横坐标为3=22﹣1，

B3的横坐标为7=23﹣1，

…

∴Bn的横坐标为2n﹣1，

∴Bn(2n﹣1，0)，

故答案为：(1，0)；(2n﹣1，0)；