题目内容
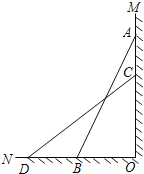
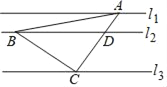
【题目】如图,直线l1∥l2∥l3,等腰直角三角形ABC的三个顶点A,B,C分别在l1,l2,l3上,∠ACB=90°,AC交l2于点D,已知l1与l2的距离为1,l2与l3的距离为3,则![]() 的值为_____.
的值为_____.
【答案】![]()
【解析】分析:先作出作BF⊥l3,AE⊥l3,再判断△ACE≌△CBF,求出CE=BF=3,CF=AE=4,然后由l2∥l3,求出DG,即可.
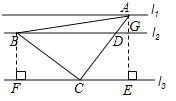
详解:如图,作BF⊥l3,AE⊥l3.
∵∠ACB=90°,∴∠BCF+∠ACE=90°.
∵∠BCF+∠CBF=90°,∴∠ACE=∠CBF.
在△ACE和△CBF中,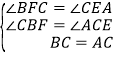 ,
,
∴△ACE≌△CBF,∴CE=BF=3,CF=AE=4.
∵l1与l2的距离为1,l2与l3的距离为3,
∴AG=1,BG=EF=CF+CE=7,
∴AB=![]() =5
=5![]() .
.
∵l2∥l3,∴![]() =
=![]() ,
,
∴DG=![]() CE=
CE=![]() ,∴BD=BG﹣DG=7﹣
,∴BD=BG﹣DG=7﹣![]() =
=![]() =
=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目
【题目】(2013年四川广安8分)某商场筹集资金12.8万元,一次性购进空调、彩电共30台.根据市场需要,这些空调、彩电可以全部销售,全部销售后利润不少于1.5万元,其中空调、彩电的进价和售价见表格.
空调 | 彩电 | |
进价(元/台) | 5400 | 3500 |
售价(元/台) | 6100 | 3900 |
设商场计划购进空调x台,空调和彩电全部销售后商场获得的利润为y元.
(1)试写出y与x的函数关系式;
(2)商场有哪几种进货方案可供选择?
(3)选择哪种进货方案,商场获利最大?最大利润是多少元?