��Ŀ����
����Ŀ���������µ�������y��a��x+1����x��4����x��Ľ���ΪA��B��A��B����ߣ�����y�ύ�ڵ�C������AC��BC��
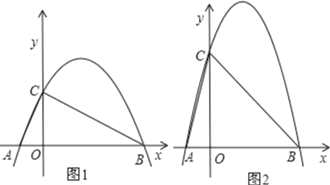
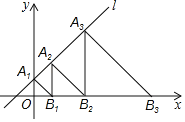
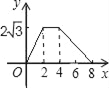
��1������ABC��ֱ�������Σ�ͼ1��������κ����Ľ���ʽ��
��2���ڣ�1���������£�����������y��ĸ���������ƽ��k��k��0������λ��ʹƽ�ƺ����������������ֻ���������㣬��k��ֵ��
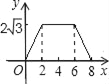
��3������C����Ϊ��0��4��ʱ��ͼ2����P��Q����ͬʱ��C���������P������COB�˶�����B����Q�������ߣ��ڵ�һ���IJ��֣��˶�����B����P��Q������˶��ٶ���ͬ������˭�ȵ����B����˵�����ɣ����ο����ݣ�![]() .6��
.6��![]() ��
��
���𰸡���1��![]() ����2��
����2��![]() ����3����P�ȵ����B��
����3����P�ȵ����B��
��������
��1��������֪�������߽���ʽ�������A��B�����꣬��Rt��ABC�У�OC��AB��������Ӱ�����ĵõ�OC2=OAOB����������������֤�ã������ɵõ�OC�ij����Ӷ�ȷ��C������꣬������������ߵĽ���ʽ�У�����ȷ��a��ֵ���Ӷ�����������ߵĽ���ʽ��
��2�����ݣ�1�����������ߵĽ���ʽ��������䶥�����꣬���ں���ͼ���ƽ�Ʒ����Ѿ�ȷ��������y�Ḻ��������ƽ�ƣ�����������������ֻ���������㣬�������������
��C��O�غϣ���ʱ����������ƽ����OC������λ��
�������ߵĶ�������x���ϣ���ʱ����������ƽ�Ƶĵ�λ�����루1���������ߵĶ�����������ͬ��
�ۺ���������������������k��ֵ��
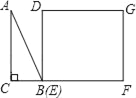
��3����C��0��4��ʱ���ɸ���������ȷ����ʱ�����ߵĽ���ʽ����������䶥��D�����ꣻP����ƶ���������ã���OC+OB������Q��Ĺ켣��һ�����ߣ���ֱ����ã������Ҫ����Ϊֱ����ӵĺ�P����ƶ�������бȽϣ�����CD��BD������B��C��D�������꣬�������CD��BD�ij����Ӷ�ȷ��BD+CDͬOC+OB�Ĵ�С��ϵ����ȻQ���ƶ�����Ҫ����CD+BD���������жϳ�P��Q�����·��˭��˭С������������ٶ���ͬ����ô·�̶̵ľ��ȵ���B�㣮
�⣺������y��a��x+1����x��4����x��Ľ���ΪA����1��0����B��4��0����
��1������ABC��ֱ�������Σ�ֻ�С�ACB��90����
�������á�ACO�ס�COB��
��![]() ��
��
��![]() ��
��
��CO��2
�������߿������£�
��C��0��2��
��C��0��2������ã�
��0+1����0��4��a��2��![]()
��![]() ��
��
��2����![]() �ɵã�
�ɵã�
�����ߵĶ���Ϊ��![]() ��
��![]() ������C��0��2����
������C��0��2����
����C����ƽ�Ƶ�ԭ��ʱ��
ƽ�ƺ����������������ֻ���������㣬
��k��2
����������ƽ�Ƶ�x��ʱ��
ƽ�ƺ����������������ֻ���������㣬
��![]() ��
��

��3������CΪ��0��4��ʱ�������ߵĽ���ʽΪy������x+1����x��4����
�����ߵĶ���ΪD��![]() ��
��![]() ��
��
����DC��DB
��D��![]() ��
��![]() ����B��4��0����C��0��4����
����B��4��0����C��0��4����
��CD��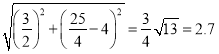 ��
��
DB�� ��
��
��CD+DB��2.7+6.75��9.45
��CO+OB��4+4��8��
��DB+DC��CO+OB
�ɺ���ͼ���֪��һ�����ڵ������ߵij��ȱ�CD+DB��Ҫ��
���Ե�һ�����ڵ������ߵij���Ҫ��������C��O��B�ij���
���Ե�P�ȵ����B��

 ���Ǽ���С����ϵ�д�
���Ǽ���С����ϵ�д� �Ͻ�ƽ���Ȿϵ�д�
�Ͻ�ƽ���Ȿϵ�д�