题目内容
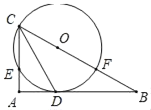
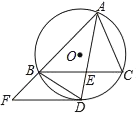
【题目】△ABC内接于⊙O,∠BAC的平分线交⊙O于D,交BC于E(BE>EC),过点D作⊙O的切线DF,交AB的延长线于F.
(1)求证:DF∥BC;
(2)连接OF,若tan∠BAC=![]() ,BD=
,BD=![]() ,DF=8,求OF的长.
,DF=8,求OF的长.
【答案】(1)证明见解析;(2)10.
【解析】
(1)根据切线的性质得:OD⊥DF,由角平分线得∠BAD=∠CAD,则所对的弧相等,由垂径定理得:OD⊥BC,从而得结论;
(2)先得∠BOD=∠BAC,根据tan∠BOD=![]() ,设ON=x,BN=
,设ON=x,BN=![]() ,利用勾股定理解决问题.
,利用勾股定理解决问题.
(1)证明:连接OD,
∵DF是⊙O的切线,
∴OD⊥DF,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴![]() ,
,
∴OD⊥BC,
∴DF∥BC;
(2)解:连接OB,
∵![]() ,
,
∴∠BOD=∠BAC,
由(1)知OD⊥BC,
∴tan∠BOD=![]() ,
,
∵tan∠BAC=2![]() ,
,
∴![]() ,
,
设ON=x,BN=2![]() x,
x,
由勾股定理得:OB=3x,
∴OD=3x,
∴DN=3x﹣x=2x,
Rt△BDN中,BN2+DN2=BD2,
∴![]() ,
,
解得x=2或﹣2(舍),
∴OB=OD=3x=6,
Rt△OFD中,由勾股定理得:OF=![]() =
=![]() =10.
=10.


练习册系列答案
相关题目