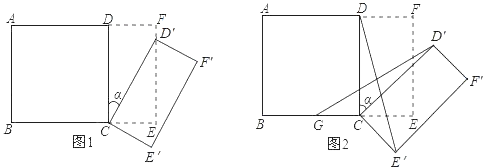
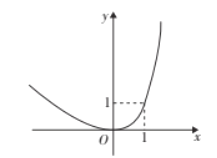
��Ŀ����
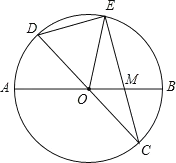
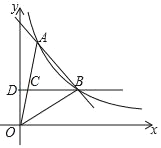
����Ŀ����ͼ��һ�κ���y��kx+b��k��0���뷴��������y��![]() ��a��0����ͼ���ڵ�һ������A��B���㣬A�������Ϊ��m��4����B�������Ϊ��3��2��������OA��OB����B��BD��y�ᣬ����ΪD����OA��C����OC��CA��
��a��0����ͼ���ڵ�һ������A��B���㣬A�������Ϊ��m��4����B�������Ϊ��3��2��������OA��OB����B��BD��y�ᣬ����ΪD����OA��C����OC��CA��
��1����һ�κ����ͷ����������ı���ʽ��
��2�����AOB�������
��3����ֱ��BD���Ƿ����һ��E��ʹ�á�AOE��ֱ�������Σ�������п��ܵ�E�����꣮
���𰸡���1��y��![]() ��y����
��y����![]() x+6����2��
x+6����2��![]() ����3��E��������
����3��E��������![]() ��2����
��2����![]() ��2����
��2����![]() ��2����
��2����![]() ��2����
��2����
��������
��1�������ô���ϵ���������������������ʽ������ȷ������A�����꣬���ô���ϵ�������һ�κ�������ʽ��
��2������A��AF��x����F��OB��G�������OB�Ľ���ʽ���������AG���������ε������ʽ���ɵó����ۣ�
��3�����������ηֱ�������⼴�ɽ�����⣻
�⣺��1���ߵ�B��3��2���ڷ���������y��![]() ��ͼ���ϣ�
��ͼ���ϣ�
��a��3��2��6��
�෴���������ı���ʽΪy��![]() ��
��
�ߵ�A��������Ϊ4��
�ߵ�A�ڷ���������y��![]() ͼ���ϣ�
ͼ���ϣ�
��A��![]() ��4����
��4����
��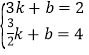 ����
����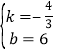 ��
��
��һ�κ����ı���ʽΪy����![]() x+6��
x+6��
��2����ͼ1������A��AF��x����F��OB��G��
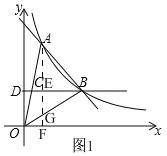
��B��3��2����
��ֱ��OB�Ľ���ʽΪy��![]() x��
x��
��G��![]() ��1����
��1����
A��![]() ��4����
��4����
��AG��4��1��3��
��S��AOB��S��AOG+S��ABG��![]() ��3��3��
��3��3��![]() ��
��
��3����ͼ2�У�
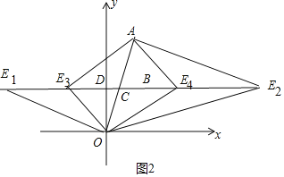
����AOE1��90��ʱ����ֱ��AC�Ľ���ʽΪy��![]() x��
x��
��ֱ��OE1�Ľ���ʽΪy����![]() x��
x��
��y��2ʱ��x����![]() ��
��
��E1����![]() ��2����
��2����
����OAE2��90��ʱ��
ֱ��OE1ƽ��ֱ��OE2
��ֱ��OE2�Ľ���ʽΪy����![]() x+b��
x+b��
��ֱ�߹���A��![]() ��4������b=
��4������b=![]()
��ֱ��OE2�Ľ���ʽΪy����![]() x+
x+![]() ��
��
��y��2ʱ��x��![]() ��
��
��E2��![]() ��2����
��2����
����OEA��90��ʱ��
��A��![]() ��4������OA=
��4������OA=![]()
��AC��OC��CE��![]() ��
��
��C��![]() ��2����
��2����
��ɵ�E3��![]() ��2����E4��
��2����E4��![]() ��2����
��2����
�������������������ĵ�E����Ϊ����![]() ��2����
��2����![]() ��2����
��2����![]() ��2����
��2����![]() ��2����
��2����

 �����ƻ���ĩ��̶�100��ϵ�д�
�����ƻ���ĩ��̶�100��ϵ�д� �ܿ���ȫ��100��ϵ�д�
�ܿ���ȫ��100��ϵ�д�