题目内容
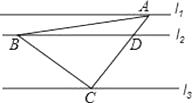
【题目】如图,已知EC∥AB,∠EDA=∠ABF. 
(1)求证:四边形ABCD是平行四边形;
(2)求证:OA2=OEOF.
【答案】
(1)证明:∵EC∥AB,
∴∠EDA=∠DAB,
∵∠EDA=∠ABF,
∴∠DAB=∠ABF,
∴AD∥BC,
∵DC∥AB,
∴四边形ABCD为平行四边形

(2)证明:∵EC∥AB,
∴△OAB∽△OED,
∴ ![]() ,
,
∵AD∥BC,
∴△OBF∽△ODA,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴OA2=OEOF.
【解析】(1)由EC∥AB,∠EDA=∠ABF,可证得∠DAB=∠ABF,即可证得AD∥BC,则得四边形ABCD为平行四边形;(2)由EC∥AB,可得 ![]() ,由AD∥BC,可得
,由AD∥BC,可得 ![]() =
= ![]() ,等量代换得出
,等量代换得出 ![]() =
= ![]() ,即OA2=OEOF.
,即OA2=OEOF.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目