题目内容
【题目】在平面直角坐标系中,一次函数y=kx+b的图象与x轴、y轴分别相交于A(﹣3,0),B(0,﹣3)两点,二次函数y=x2+mx+n的图象经过点A.
(1)求一次函数y=kx+b的解析式;
(2)若二次函数y=x2+mx+n图象的顶点在直线AB上,求m,n的值;
(3)当﹣3≤x≤0时,二次函数y=x2+mx+n的最小值为﹣4,求m,n的值.
【答案】
(1)
解:A(﹣3,0),B(0,﹣3)代入y=kx+b得
![]() ,解得
,解得 ![]() ,
,
∴一次函数y=kx+b的解析式为:y=﹣x﹣3
(2)
解:二次函数y=x2+mx+n图象的顶点为(﹣ ![]() ,
, ![]() )
)
∵顶点在直线AB上,
∴ ![]() =
= ![]() ﹣3,
﹣3,
又∵二次函数y=x2+mx+n的图象经过点A(﹣3,0),
∴9﹣3m+n=0,
∴组成方程组为 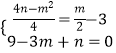
解得 ![]() 或
或 ![]()
(3)
解:∵二次函数y=x2+mx+n的图象经过点A.
∴9﹣3m+n=0,
∵当﹣3≤x≤0时,二次函数y=x2+mx+n的最小值为﹣4,
①如图1,当对称轴﹣3<﹣ ![]() <0时
<0时

最小值为 ![]() =﹣4,与9﹣3m+n=0,组成方程组为
=﹣4,与9﹣3m+n=0,组成方程组为
 解得
解得 ![]() 或
或 ![]() (由﹣3<﹣
(由﹣3<﹣ ![]() <0知不符合题意舍去)
<0知不符合题意舍去)
所以 ![]() .
.
②如图2,当对称轴﹣ ![]() >0时,在﹣3≤x≤0时,x为0时有最小值为﹣4,
>0时,在﹣3≤x≤0时,x为0时有最小值为﹣4,

把(0,﹣4)代入y=x2+mx+n得n=﹣4,
把n=﹣4代入9﹣3m+n=0,得m= ![]() .
.
∵﹣ ![]() >0,
>0,
∴m<0,
∴此种情况不成立,
③当对称轴﹣ ![]() =0时,y=x2+mx+n的最小值为﹣4,
=0时,y=x2+mx+n的最小值为﹣4,
把(0,﹣4)代入y=x2+mx+n得n=﹣4,
把n=﹣4代入9﹣3m+n=0,得m= ![]() .
.
∵﹣ ![]() =0,
=0,
∴m=0,
∴此种情况不成立,
④当对称轴﹣ ![]() ≤﹣3时,最小值为0,不成立
≤﹣3时,最小值为0,不成立
综上所述m=2,n=﹣3.
【解析】(1)利用待定系数法求出解析式,(2)先表示出二次函数y=x2+mx+n图象的顶点,利用直线AB列出式子,再与点A在二次函数上得到的式子组成方程组求得m,n的值,(3)本题要分四种情况①当对称轴﹣3<﹣ ![]() <0时,②当对称轴﹣
<0时,②当对称轴﹣ ![]() >0时,③当对称轴﹣
>0时,③当对称轴﹣ ![]() =0时,④当对称轴﹣
=0时,④当对称轴﹣ ![]() ≤﹣3时,结合二次函数y=x2+mx+n的图象经过点A得出的式子9﹣3m+n=0,求出m,n但一定要验证是否符合题意.
≤﹣3时,结合二次函数y=x2+mx+n的图象经过点A得出的式子9﹣3m+n=0,求出m,n但一定要验证是否符合题意.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案