题目内容
【题目】已知二次函数![]() 的图象过点
的图象过点![]() 且与直线
且与直线![]() 相交于
相交于![]() 、
、![]() 两点,点
两点,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上.
轴上.
![]() 求二次函数的解析式.
求二次函数的解析式.
![]() 如果
如果![]() 是线段
是线段![]() 上的动点,
上的动点,![]() 为坐标原点,试求
为坐标原点,试求![]() 的面积
的面积![]() 与
与![]() 之间的函数关系式,并求出自变量的取值范围.
之间的函数关系式,并求出自变量的取值范围.
![]() 是否存在这样的点
是否存在这样的点![]() ,使
,使![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】:![]() ;
;![]() ;
;![]() 不存在点
不存在点![]() ,使PO=AO=2.理由见解析.
,使PO=AO=2.理由见解析.
【解析】
(1)先确定直线![]() 与
与![]() 轴的交点
轴的交点![]() 的坐标为
的坐标为![]() ,与
,与![]() 轴的交点
轴的交点![]() 的坐标为
的坐标为![]() ,然后利用待定系数法求二次函数的解析式;
,然后利用待定系数法求二次函数的解析式;
(2)根据三角形面积公式得到![]() ,然后利用
,然后利用![]() 的函数关系用x表示S即可;
的函数关系用x表示S即可;
(3)先利用勾股定理计算出BC,再利用面积法求出O点到BC的距离OD=2.4,则点P到O点的最短距离为2.4,所以不存在点P,使PO=AO=2.
![]() 直线
直线![]() 与
与![]() 轴的交点
轴的交点![]() 的坐标为
的坐标为![]() ,与
,与![]() 轴的交点
轴的交点![]() 的坐标为
的坐标为![]() ,
,
把![]() 、
、![]() 、
、![]() 代入
代入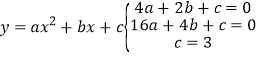 ,
,
解得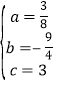 ,
,
所以二次函数的解析式为![]() ;
;
![]() ;
;
![]() 不存在.理由如下:
不存在.理由如下:
作![]() ,如图,
,如图,
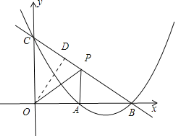
∵![]() 、
、![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴点![]() 到
到![]() 点的最短距离为
点的最短距离为![]() ,
,
∴不存在点![]() ,使
,使![]() .
.

练习册系列答案
相关题目




