题目内容
【题目】已知函数y1=x﹣m+1和y2=![]() (n≠0)的图象交于P,Q两点.
(n≠0)的图象交于P,Q两点.
(1)若y1的图象过(n,0),且m+n=3,求y2的函数表达式:
(2)若P,Q关于原点成中心对称.
①求m的值;
②当x>2时,对于满足条件0<n<n0的一切n总有y1>y2,求n0的取值范围.
【答案】(1)y2=![]() ;(2)①m=1;②0<n0≤4.
;(2)①m=1;②0<n0≤4.
【解析】
(1)把(n,0)代入y1=x﹣m+1,得0=n﹣m+1,结合即可求出m和n的值,从而可求出y2的解析式;
(2)①设P(x,y),由P,Q关于原点成中心对称,可知Q(﹣x,﹣y),由P,Q关于原点成中心对称,把P和Q的坐标代入y1=x﹣m+1即可求出m的值;
②当m=1时,y1=x,由当x>2时,对于满足条件0<n<n0的一切n总有y1>y2,可得x>![]() ,即x2>n,且x>2,从而可求出n0的取值范围.
,即x2>n,且x>2,从而可求出n0的取值范围.
(1)∵若y1的图象过(n,0),
∴0=n﹣m+1 且m+n=3,
∴m=2,n=1,
∴y2的函数表达式:y2=![]() ;
;
(2)①设P(x,y),
∵P,Q关于原点成中心对称,
∴Q(﹣x,﹣y).
∵函数y1=x﹣m+1和y2=![]() (n≠0)的图象交于P,Q两点,
(n≠0)的图象交于P,Q两点,
∴y=x﹣m+1,
∴﹣y=﹣x﹣m+1,
∴m=1;
②当m=1时,y1=x,
∵当x>2时,对于满足条件0<n<n0的一切n总有y1>y2,
∴x>![]() ,
,
∴x2>n,且x>2,
∴n<4,
∴0<n0≤4;

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
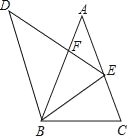
【题目】如图,在△ABC中,∠A=36°,AC=AB=2,将△ABC绕点B逆时针方向旋转得到△DBE,使点E在边AC上,DE交AB于点F,则△AFE与△DBF的面积之比等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()