题目内容
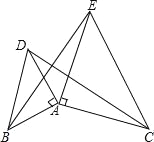
【题目】已知,如图,△ABC,∠ACB=90°,∠B=2∠A.
(1)用直尺和圆规作△ABC的角平分线BD,保留作图痕迹;
(2)在(1)的基础上,求∠ADB的度数.

【答案】(1)见解析;(2)∠ADB=120°.
【解析】
(1)根据尺规作角平分线的步骤作图即可;
(2)根据∠ACB=90°,∠B=2∠A可求出∠A=30°,∠ABC=60°,根据角平分线定义可得∠ABD=30°,然后由三角形内角和定理可得答案.
解:(1)如图,线段BD即为所求.

(2)因为∠ACB=90°,
所以∠A+∠ABC=90°,
因为∠ABC=2∠A,
所以∠A=30°,∠ABC=60°,
又因为BD平分∠ABC,
所以∠ABD=![]() ∠ABC=30°,
∠ABC=30°,
因为∠ADB+∠A+∠ABD=180°,
所以∠ADB=180°-30°-30°=120°.

练习册系列答案
相关题目
【题目】某校举办“红歌伴我成长”歌咏比赛活动,参赛同学的成绩分别绘制成频数分布表和频数分布直方图(均不完整)如图:
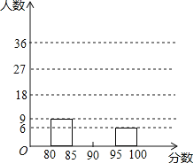
分数段 | 频数 | 频率 |
80≤x<85 | 9 | 0.15 |
85≤x<90 | m | 0.45 |
90≤x<95 | ■ | ■ |
95≤x<100 | 6 | n |
(1)求m,n的值分别是多少;
(2)请在图中补全频数分布直方图;
(3)比赛成绩的中位数落在哪个分数段?