题目内容
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() 为
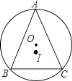
为![]() 外接圆,
外接圆,![]() 为
为![]() 的内心.
的内心.
![]() 求
求![]() 的长;
的长;
![]() 求
求![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
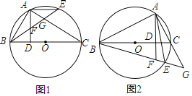
(1)连接AO,且延长AO交BC于D,连接OB、OC,求出AD⊥BC,BD=DC,根据勾股定理求出AD.在Rt△OBD中,由勾股定理得出OB2=OD2+BD2,代入求出即可;
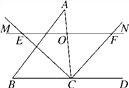
(2)作△ABC的内切圆I,过点I作ID⊥BC,垂足为D.先利用面积法求得ID=![]() ,然后再Rt△BDI中依据勾股定理求得IB的长即可.
,然后再Rt△BDI中依据勾股定理求得IB的长即可.
(1)如图1所示:连接AO,且延长AO交BC于D,连接OB、OC.
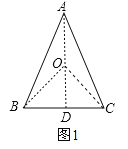
∵AB=AC,O为△ABC外接圆的圆心,∴AD⊥BC,BD=DC,BD=DC=![]() BC=5,设等腰△ABC外接圆的半径为R,则OA=OB=OC=R.在Rt△ABD中,由勾股定理得:AD=12.在Rt△OBD中,由勾股定理得:OB2=OD2+BD2,即R2=(12﹣R)2+52,解得:R=
BC=5,设等腰△ABC外接圆的半径为R,则OA=OB=OC=R.在Rt△ABD中,由勾股定理得:AD=12.在Rt△OBD中,由勾股定理得:OB2=OD2+BD2,即R2=(12﹣R)2+52,解得:R=![]() ,∴BO=
,∴BO=![]() ;
;
(2)如图2所示:作△ABC的内切圆I,过点I作ID⊥BC,垂足为D.
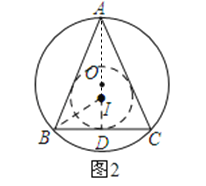
设圆I的半径为r,根据题意得:![]() ,即
,即![]() .解得:r=
.解得:r=![]() .
.
∵BC是圆I的切线,∴ID⊥BC.
在Rt△BID中,由勾股定理得:BI=![]() =
=![]() =
=![]() .
.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目