题目内容
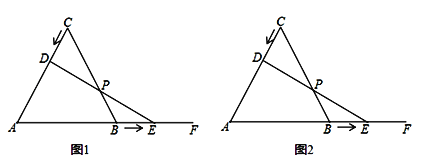
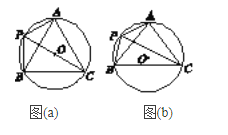
【题目】如图所示,在平面直角坐标系中,△ABC是⊙O的内接三角形,AB=AC,点P是![]() 的中点,连结PA,PB,PC.
的中点,连结PA,PB,PC.
(1)如图(a),若∠BPC=60°,求证:AC=![]() AP;
AP;
(2)如图(b),若sin∠BPC=![]() ,求tan∠PAB的值.
,求tan∠PAB的值.
【答案】(1)详见解析;(2)tan∠PAB=![]() .
.
【解析】
(1)利用已知条件易证△ABC为等边三角形,所以∠ACB=60°,因为点P是弧AB的中点,所以∠ACP=30°,进而证明AC=![]() AP;
AP;
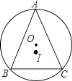
(2)①由等腰三角形的性质可得∠BAC=2∠CAF,由圆周角定理可得∠FOC=2∠CAF,进而可证明∠FOC=∠BAC;
②过点E作EG⊥AC于G,连接OC,设FC=24a,则OC=OA=25a,因为OF=7a,AF=32a.在Rt△AFC中,AC2=AF2+FC2,所以AC=40a,进而可求出tan∠PAB的值.
解:(1)证明:∵∠BAC=∠BPC=60°.
又∵AB=AC,
∴△ABC为等边三角形,
∴∠ACB=60°,
∵点P是![]() 的中点,
的中点,
∴∠ACP=30°,
又∵∠APC=∠ABC=60°,
∴AC=![]() AP.
AP.
(2)如图,连结AO并延长交PC于点E,交BC于点F,过点E作EG⊥AC于点G,连结OC.

∵AB=AC,
∴AF⊥BC,BF=CF.
又∵点P是![]() 的中点,
的中点,
∴∠ACP=∠PCB,
∴EG=EF.
∵∠BPC=∠BAC,
又∵∠BAC=∠FOC,
∴∠BPC=∠FOC,
∴sin∠FOC=sin∠BPC=![]() .
.
设FC=24a,则OC=OA=25a,
∴OF=7a,AF=32a.
在Rt△AFC中,AC2=AF2+FC2,∴AC=40a.
在Rt△AGE和Rt△AFC中,sin∠FAC=![]() ,
,
∴![]() ,∴EG=12a.
,∴EG=12a.
∴tan∠PAB=tan∠PCB=![]() .
.

练习册系列答案
相关题目