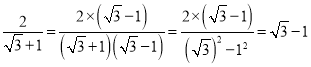题目内容
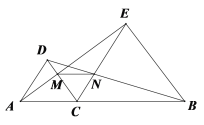
【题目】如图,在四边形ABCD中,![]() ,AE交BC于点P,交DC的延长线于点E,点P为AE的中点.
,AE交BC于点P,交DC的延长线于点E,点P为AE的中点.
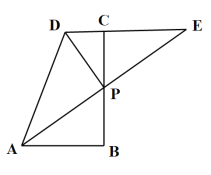
(1)求证:点P也是BC的中点.
(2)若![]() ,且
,且![]() ,求AP的长.
,求AP的长.
(3)在(2)的条件下,若线段AE上有一点Q,使得![]() 是等腰三角形,求
是等腰三角形,求![]() 的长.
的长.
【答案】(1)证明见详解;(2)5;(3)4或![]() 或
或![]() .
.
【解析】
(1)由![]() ,得∠B=∠ECP,由点P为AE的中点,得AP=EP,根据AAS可证CEPBAP,进而得到结论;
,得∠B=∠ECP,由点P为AE的中点,得AP=EP,根据AAS可证CEPBAP,进而得到结论;
(2)在RtDCP中,利用勾股定理,可得CP的长,即BP的长,从而在RtABP中,利用勾股定理,即可求解;
(3)若![]() 是等腰三角形,分3种情况讨论:①当AQ=AB时,②当BQ=AB时,③当AQ=BQ时,分别根据等腰三角形的性质和勾股定理求出AQ的值即可.
是等腰三角形,分3种情况讨论:①当AQ=AB时,②当BQ=AB时,③当AQ=BQ时,分别根据等腰三角形的性质和勾股定理求出AQ的值即可.
(1)∵![]() ,
,
∴∠B=∠ECP,
∵点P为AE的中点,
∴AP=EP,
在CEP和BAP中,
∵ (对顶角相等)
(对顶角相等)
∴CEPBAP(AAS)
∴BP=CP,
∴点P也是BC的中点;
(2)∵![]() ,
,![]()
∴![]() ,
,
∴![]()
![]() ,
,
∴BP=CP=3,
∴在RtABP中,![]()
(3)若![]() 是等腰三角形,分3种情况讨论:
是等腰三角形,分3种情况讨论:
①当AQ=AB时,如图1,
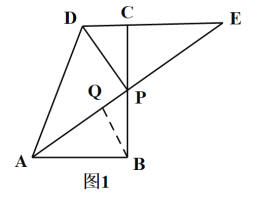
∵AB=4,
∴AQ=4;
②当BQ=AB时,如图2,

过段B作BM⊥AE于点M,
∵在RtABP中,AB=4,BP=3,AP=5,
∴BM=![]() ,
,
∵在RtABM中,![]() ,
,
∴![]() ,
,
∵BQ=AB,BM⊥AE,
∴MQ=AM=![]() ,
,
∴AQ=2×![]() =
=![]() ,
,
③当AQ=BQ时,
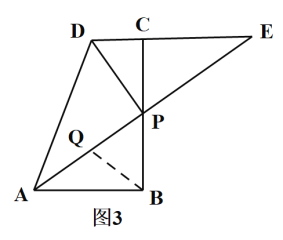
∴∠QAB=∠QBA,
∵![]() ,
,
∴∠QAB+∠QPB=90°,∠QBA+∠QBP=90°,
∴∠QPB=∠QBP,
∴BQ=PQ,
∴AQ= BQ=PQ=![]() AP=
AP=![]() ×5=
×5=![]() ;
;
综上所述,AQ的长为:4或![]() 或
或![]() .
.

练习册系列答案
相关题目