题目内容
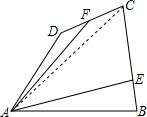
如图，在四边形ABCD，点E，F分别在BC，CD上，DF=FC，CE=2EB，已知S△ADF=m，SAECF=n（n＞m），求四边形ABCD的面积．
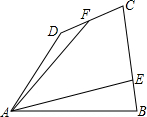
如图，连接AC，∵DF=FC，
∴S△ADF=S△ACF=m，
∵SAECF=n，
∴S△ACE=n-m，
∵CE=2EB，
∴S△ABE=
S△ACE=
（n-m），
∴四边形ABCD的面积=S△ADF+SAECF+S△ABE=m+n+
（n-m）=
m+
n．
故答案为：
m+
n．
∴S△ADF=S△ACF=m，
∵SAECF=n，
∴S△ACE=n-m，
∵CE=2EB，
∴S△ABE=
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形ABCD的面积=S△ADF+SAECF+S△ABE=m+n+
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
故答案为：
| 1 |
| 2 |
| 3 |
| 2 |
练习册系列答案
相关题目
