题目内容
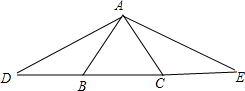
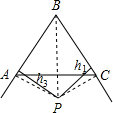
已知等边△ABC外有一点P，设P到BC、CA、AB的距离分别为h1，h2，h3，且h1-h2+h3=6，那么等边△ABC的面积为______．
设等边△ABC的边长为a，连接PA、PB、PC，
则S△PAB+S△PBC-S△PAC=S△ABC，
从而
ah1-
ah2+
ah3=
a2，
即
a（h1-h2+h3）=
a2，
∵h1-h2+h3=6，
∴a=4
，
∴S△ABC=
a2=12
．
故答案为12
．
则S△PAB+S△PBC-S△PAC=S△ABC，
从而
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 4 |
即
| 1 |
| 2 |
| ||
| 4 |
∵h1-h2+h3=6，
∴a=4
| 3 |
∴S△ABC=
| ||
| 4 |
| 3 |
故答案为12
| 3 |
练习册系列答案
轻松课堂单元测试AB卷系列答案
小题狂做系列答案
相关题目
