题目内容
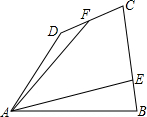
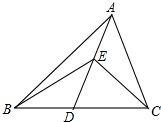
如图，在△ABC中，已知D是边BC上一点，满足AD=AC，E是边AD的中点，满足∠BAD=∠ACE，若S△BDE=2，则S△ABC为______．
∵E是AD的中点，
∴S△ABD=2S△BDE=4（等高，底边AD=2DE），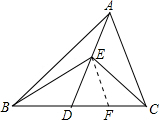
取CD中点F，连接EF，
∵E为AD中点，F为DC中点，
∴EF∥AC，
∴∠ACE=∠FEC，∠EFD=∠ACD，
∵∠BAD=∠ACE，
∴∠BAD=∠CEF，
∵AC=AD，
∴∠ADF=∠ACD，
∴∠EDF=∠EFD，
∴∠ADB=∠EFC，
∴△ABD∽△CEF，
∴
=
=2，
∴S△CEF=
S△ABD=1，
又∵△CEF与△ACE等高，底边AC=2EF，
∴S△ACE=2S△CEF=2，
∴S△ADC=2S△ACE=4，
故S△ABC=S△ABD+S△ACD=8．
故答案为：8．
∴S△ABD=2S△BDE=4（等高，底边AD=2DE），
取CD中点F，连接EF，
∵E为AD中点，F为DC中点，
∴EF∥AC，
∴∠ACE=∠FEC，∠EFD=∠ACD，
∵∠BAD=∠ACE，
∴∠BAD=∠CEF，
∵AC=AD，
∴∠ADF=∠ACD，
∴∠EDF=∠EFD，
∴∠ADB=∠EFC，
∴△ABD∽△CEF，
∴
| AC |
| EF |
| AD |
| EF |
∴S△CEF=
| 1 |
| 4 |
又∵△CEF与△ACE等高，底边AC=2EF，
∴S△ACE=2S△CEF=2，
∴S△ADC=2S△ACE=4，
故S△ABC=S△ABD+S△ACD=8．
故答案为：8．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
