Question

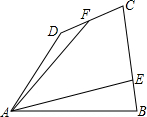
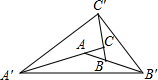
如图所示，在四边形ABCD中，AM=MN=ND，BE=EF=FC，四边形ABEM，MEFN，NFCD的面积分别记为S₁，S₂和S₃，求

S2

S1+S3

=？
（提示：连接AE、EN、NC和AC）

Answer 1

如图a所示：连接AE、EN和NC，设四边形AECN的面积为S，
∵AM=MN=ND，BE=EF=FC，
∴S_△AEM=S_△MEN，S_△CNF=S_△EFN，
上面两个式子相加得S_△AEM+S_△CNF=S₂
并且四边形AECN的面积S=2S₂，即：S₂=

1

2

S，S_△AEM+S_△CNF=

1

2

S．
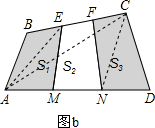
连接AC，如图b所示：
∵AM=MN=ND，BE=EF=FC，
∴CE=2BE，NA=2DN，
∴S_△ABE=

1

2

S_△AEC，S_△CDN=

1

2

S_△CNA，
上面两个式子相加得S_△ABE+S_△CDN=

1

2

×四边形AECN的面积=

1

2

S，
所以，S_△AEM+S_△CNF+S_△ABE+S_△CDN=

1

2

S+

1

2

S=S，
因此S₁+S₃=S，

S2

S1+S3

=

1 2 S

S

=

1

2

．
答：

S2

S1+S3

=

1

2

．