题目内容
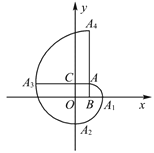
【题目】已知抛物线y=a(x﹣m)2+2m(m≠0)经过原点,其顶点为P,与x轴的另一交点为A.
(1)P点坐标为 ,A点坐标为 ;(用含m的代数式表示)
(2)求出a,m之间的关系式;
(3)当m>0时,若抛物线y=a(x﹣m)2+2m向下平移m个单位长度后经过点(1,1),求此抛物线的表达式;
(4)若抛物线y=a(x﹣m)2+2m向下平移|m|个单位长度后与x轴所截的线段长,与平移前相比有什么变化?请直接写出结果.
【答案】(1)(m,2m),(2m,0);(2)a=﹣![]() ;(3)y=﹣(x﹣2)2+4或y=﹣2(x﹣1)2+2;(4)与x轴所截的线段长,与平移前相比是原来的
;(3)y=﹣(x﹣2)2+4或y=﹣2(x﹣1)2+2;(4)与x轴所截的线段长,与平移前相比是原来的![]() 或
或![]() 倍.
倍.
【解析】
(1)根据抛物线的顶点式即可求得P的坐标,得出对称轴为x=m,然后根据抛物线的对称性求得A的坐标;
(2)将x=0,y=0代入y=a(x﹣m)2+2m,化简即可求得a,m之间的关系式;
(3)先表示出当m>0时,抛物线y=a(x﹣m)2+2m向下平移m个单位长度后的解析式,再将点(1,1)代入,结合(2)中a和m的关系式,解得a和m的值,即可得出此抛物线的表达式;
(4)分两种情况:①a=﹣![]() ,m>0,a<0,②m<0,a>0,a=﹣
,m>0,a<0,②m<0,a>0,a=﹣![]() ,分别得出平移后的抛物线与坐标轴的交点,然后用含m的式子表示出与x轴所截的线段长,两者相比即可求得答案.
,分别得出平移后的抛物线与坐标轴的交点,然后用含m的式子表示出与x轴所截的线段长,两者相比即可求得答案.
解:(1)∵抛物线y=a(x﹣m)2+2m(m≠0),
∴P(m,2m),
∴对称轴为直线x=m,
∵抛物线y=a(x﹣m)2+2m(m≠0)经过原点,
∴A(2m,0).
故答案为:(m,2m),(2m,0).
(2)将x=0,y=0代入y=a(x﹣m)2+2m,得am2+2m=0,m≠0,
∴am+2=0.
∴am=﹣2,
∴a=﹣![]() .
.
(3)当m>0时,抛物线y=a(x﹣m)2+2m向下平移m个单位长度后,得y=a(x﹣m)2+m.
∵抛物线经过点(1,1),
∴a(1﹣m)2+m=1,
∴am2﹣2am+a+m=1.
又∵am=﹣2,
∴a=m﹣3.
把a=m﹣3代入am=﹣2,
解得a1=﹣1,m1=2或a2=﹣2,m2=1.
∴此抛物线的表达式为y=﹣(x﹣2)2+4或y=﹣2(x﹣1)2+2.
(4)①∵a=﹣![]()
∴当m>0时,a<0,
∵抛物线y=a(x﹣m)2+2m(m≠0)经过原点
∴y=ax2﹣2amx
向下平移m个单位后为y=ax2﹣2amx﹣m
平移前d=2m
平移后:令ax2﹣2amx﹣m=0得:
a(x﹣m)2=am2+m
化简得:(x﹣m)2=![]()
∴x1=m﹣![]() ,x2=m+
,x2=m+![]() m
m
∴d'=![]() m
m
∴![]() =
=![]() ;
;
②当m<0时,a>0,a=﹣![]()
原抛物线为y=ax2﹣2amx,向下平移|m|个单位后为y=ax2﹣2amx+m
平移前d=﹣2m
平移后:令ax2﹣2amx+m=0得:
a(x﹣m)2=am2+m
化简得:(x﹣m)2=![]() m2
m2
解得:x1=m﹣![]() m,x2=m+
m,x2=m+![]() m
m
∴d'=﹣![]() m
m
∴![]() =
=![]()
综上所述,与x轴所截的线段长,与平移前相比是原来的![]() 或
或![]() 倍.
倍.