题目内容
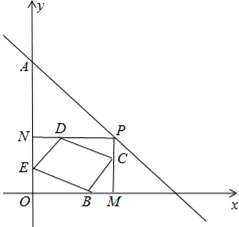
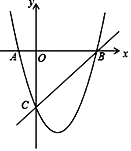
【题目】如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(﹣1,0),B(4,0),C(0,﹣4)三点,点P是直线BC下方抛物线上一动点.
(1)求这个二次函数的解析式;
(2)动点P运动到什么位置时,△PBC面积最大,求出此时P点坐标和△PBC的最大面积.
【答案】(1)y=x2-3x-4;(2)P点坐标(2,-6)时, △PBC的最大面积为8.
【解析】
解析
(1)由A,B,C三点的坐标,利用待定系数法可求得抛物线解析式;
(2)过P作PE⊥x轴,交x轴于点E,交直线BC于点F,用P点坐标可表示出PF的长,则可表示出△PBC的面积,利用二次函数的性质可求得△PBC面积的最大值及P点的坐标.
解:(1)设抛物线解析式为y=ax2+bx+c,把A,B,C三点坐标代入可得
 ,计算得出
,计算得出 ,
,
![]() 抛物线解析株式为y= x2-3x-4;
抛物线解析株式为y= x2-3x-4;
(2)![]() 点P在抛物线上,
点P在抛物线上,![]() 可设P(t,t2-3t-4),
可设P(t,t2-3t-4),
过P作 PE⊥x轴于点E,交直线BC于点F,如图

![]() B(4,0),C(0,-4),
B(4,0),C(0,-4),![]() 直线BC解析式为y=x-4,
直线BC解析式为y=x-4,
![]() F(t,t-4),
F(t,t-4),
![]() PF=(t-4)-(t2-3t-4)=-t2+4t,
PF=(t-4)-(t2-3t-4)=-t2+4t,
![]()
![]() =
=![]() +
+![]() =
=![]() PF
PF![]() OD+
OD+![]() PF
PF![]() BE=
BE=![]() PF
PF![]() (OE+BE)=
(OE+BE)=
![]() (-t2+4t)
(-t2+4t)![]() 4=-2(t-2) 2+8,
4=-2(t-2) 2+8,
![]() 当t=2时,
当t=2时, ![]() 最大值为8,此时t2-3t-4=-6,
最大值为8,此时t2-3t-4=-6,
![]() 当P点坐标为(2,-6)时,△PBC的最大面积为8.
当P点坐标为(2,-6)时,△PBC的最大面积为8.

练习册系列答案
相关题目