题目内容
【题目】如图,AB是⊙O的直径,NM与⊙O相切于点M,与AB的延长线交于点N,MH⊥AB于点H.
(1)求证:∠1=∠2;
(2)若∠N=30°,BN=5,求⊙O的半径;
(3)在(2)的条件下,求线段BN、MN及劣弧BM围成的阴影部分面积.
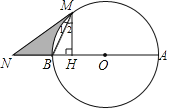
【答案】(1)详见解析;(2)⊙O的半径为5;(3)![]()
【解析】
(1)根据切线的性质得出OM⊥MN,即可得出∠1+∠BMO=∠NMO=90°,由NH⊥AB,推出∠2+∠MBO=90°,根据等腰三角形的性质得出∠OBM=∠OMB,即可证得∠1=∠2;
(2)由∠N=30°,推出∠1+∠2=60°,所以∠1=∠2=30°,∠MON=60°,得到BM=BN=5,易知△OBM为等边三角形,所以OB=OM=BM=5,得出结论;
(3)三角形OMN的面积减去扇形OMN的面积即为线段BN、MN及劣弧BM围成的阴影部分面积.
解:(1)证明:连接OM,
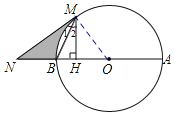
∵NM与⊙O相切,
∴OM⊥MN,
∵OB=OM,
∴∠OBM=∠OMB,
∵NH⊥AB,
∴∠2+∠MBO=90°,
∵∠1+∠BMO=∠NMO=90°,
∴∠1=∠2;
(2)∵∠N=30°,
MH⊥AB,
∴∠1+∠2=60°,
∴∠1=∠2=30°,∠MON=60°,
∴BM=BN=5,
∵OB=OM,
∴△OBM为等边三角形,
∴OB=OM=BM=5,
即⊙O的半径为5;
(3)由(2)知,∠N=30°,OM=5,
∴MN=5![]() ,
,
∴S△OMN=![]() MNOM=
MNOM=![]() =
=![]() ,
,
S扇形MOB=![]() =
=![]() ,
,
∴线段BN、MN及劣弧BM围成的阴影部分面积=![]() .
.

练习册系列答案
相关题目