Question

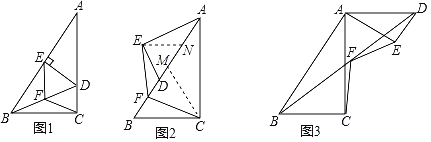
【题目】如图1，△ABC是直角三角形，∠ACB＝90°，点D在AC上，DE⊥AB于E，连接BD，点F是BD的中点，连接EF，CF．

（1）EF和CF的数量关系为　 　；

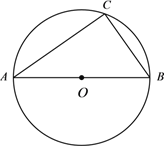
（2）如图2，若△ADE绕着点A旋转，当点D落在AB上时，小明通过作△ABC和△ADE斜边上的中线CM和EN，再利用全等三角形的判定，得到了EF和CF的数量关系，请写出此时EF和CF的数量关系　 　；

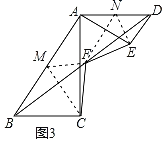
（3）若△AED继续绕着点A旋转到图3的位置时，EF和CF的数量关系是什么？写出你的猜想，并给予证明．

Answer 1

【答案】（1）EF=CF；（2）EF=CF；（3）EF=CF，证明详见解析．

【解析】

（1）根据DE⊥AB，可得∠ACB＝∠DEB＝90°，再根据中点平分线段长度可得EF＝CF＝BD，即可证明EF＝CF；

（2）根据三角形斜边中线定理可得CM＝BM＝AM＝AB，AN＝EN＝DN＝AD，即可推出FM＝EN，再根据旋转的性质得ENF＝∠CMF，即可证明△EFN≌△FCM（SAS），得证EF＝CF；

（3）取AB的中点M，AD的中点N，连接MC，MF，EN，FN，通过证明四边形MFNA是平行四边形，可得NF＝AM，∠FMA＝∠ANF，再通过三角形斜边中线定理和角的和差关系可得CM＝NF，即可证明△MFC≌△NEF（SAS），从而得证FE＝FC．

解：（1）EF＝CF，

理由：∵DE⊥AB，

∴∠ACB＝∠DEB＝90°，

∵F是BD的中点，

∴EF＝CF＝BD；

故答案为：EF＝CF；

（2）EF＝CF，

理由：∵∠AED＝∠ACB＝90°，CM和EN是△ABC和△ADE斜边上的中线，

∴CM＝BM＝AM＝AB，AN＝EN＝DN＝AD，

∵点F是BD的中点，

∴BF＝FD，

∴AN+BF＝DN+DF＝FN＝AB，

∴FN＝CM＝AM，

∵FM＝FN﹣MN，AN＝AM﹣MN，

∴FM＝AN，

∴FM＝EN，

∵△ADE绕着点A旋转，当点D落在AB上，

∴∠EAD＝∠CAB，

∵∠EAN＝∠AEN，∠MAC＝∠ACM，

∴∠ENF＝∠EAN+∠AEN＝2∠EAN，∠CMF＝∠CAM+∠ACM＝2∠CAM，

∴∠ENF＝∠CMF，

在△EFN与△FCM中，，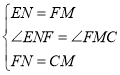

∴△EFN≌△FCM（SAS），

∴EF＝CF；

故答案为：EF＝CF；

（3）猜想，EF＝CF，

理由：如图3中，取AB的中点M，AD的中点N，连接MC，MF，EN，FN．

∵BM＝MA，BF＝FD，

∴MF∥AD，MF＝AD，

∵AN＝ND，

∴MF＝AN，MF∥AN，

∴四边形MFNA是平行四边形，

∴NF＝AM，∠FMA＝∠ANF，

在Rt△ADE中，∵AN＝ND，∠AED＝90°，

∴EN＝AD＝AN＝ND，同理CM＝AB＝AM＝MB，

在△AEN和△ACM中，

∠AEN＝∠EAN，∠MCA＝∠MAC，

∵∠MAC＝∠EAN，

∴∠AMC＝∠ANE，

又∵∠FMA＝∠ANF，

∴∠ENF＝∠FMC，

∵AM＝FN，AM＝CM，

∴CM＝NF，

在△MFC和△NEF中，，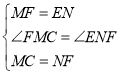

∴△MFC≌△NEF（SAS），

∴FE＝FC．