جâؤ؟ؤعبف
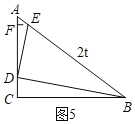
،¾جâؤ؟،؟بçح¼£¬شع،÷ABCضذ£¬،دC=90،م£¬AB=5cm£¬cosB![]() £®¶¯µمD´سµمA³ِ·¢رط×إةندكACµؤ·½دٍزشأ؟أë1cmµؤثظ¶بزئ¶¯£¬¶¯µمE´سµمB³ِ·¢رط×إةندكBAµؤ·½دٍزشأ؟أë2cmµؤثظ¶بزئ¶¯£®زرضھµمD؛حµمEح¬ت±³ِ·¢£¬ةèثüأاشث¶¯µؤت±¼نخھtأ룮ءھ½لBD£®
£®¶¯µمD´سµمA³ِ·¢رط×إةندكACµؤ·½دٍزشأ؟أë1cmµؤثظ¶بزئ¶¯£¬¶¯µمE´سµمB³ِ·¢رط×إةندكBAµؤ·½دٍزشأ؟أë2cmµؤثظ¶بزئ¶¯£®زرضھµمD؛حµمEح¬ت±³ِ·¢£¬ةèثüأاشث¶¯µؤت±¼نخھtأ룮ءھ½لBD£®
£¨1£©µ±AD=ABت±£¬اَtan،دABDµؤضµ£»
£¨2£©زشAخھش²ذؤ£¬ADخھ°ë¾¶»،رA£»زشµمBخھش²ذؤ،¢BEخھ°ë¾¶»،رB£®جضآغ،رAسë،رBµؤخ»ضأ¹طدµ£¬²¢ذ´³ِدà¶شس¦µؤtµؤضµ£®
£¨3£©µ±،÷BDEخھض±½اب½اذخت±£¬ض±½سذ´³ِtan،دCBDµؤضµ£®

،¾´ً°¸،؟£¨1£©2£»£¨2£©¢ظµ±ء½ش²حâہëت±£¬![]() £»¢عµ±ء½ش²حâاذت±£¬
£»¢عµ±ء½ش²حâاذت±£¬![]() £»¢غµ±ء½ش²دཻت±£¬
£»¢غµ±ء½ش²دཻت±£¬![]() £»¢ـµ±ء½ش²ؤعاذت±£¬t=5£»¢فµ±ء½ش²ؤع؛¬ت±£¬t£¾5£»£¨3£©tan،دCBDµؤضµتا
£»¢ـµ±ء½ش²ؤعاذت±£¬t=5£»¢فµ±ء½ش²ؤع؛¬ت±£¬t£¾5£»£¨3£©tan،دCBDµؤضµتا![]() »ٍ
»ٍ![]() »ٍ
»ٍ![]() »ٍ
»ٍ![]() £®
£®
،¾½âخِ،؟
£¨1£©دب¸ù¾فب½ا؛¯ت¶¨زه؟ةµأBC£½4£¬سة¹´¹ة¶¨ہي¼ئثمAC£½3£¬×î؛َض¤أ÷،دABD£½،دD£¬¼ئثم،دDµؤصاذ¼´؟ة£»
£¨2£©·ضاé؟ِجضآغ£¬¸ù¾فء½ش²حâہ룬حâاذ£¬دཻ£¬ؤعاذ£¬ؤع؛¬µؤ¶¨زه؟ةµأ½لآغ£»
£¨3£©µ±،÷BDEخھض±½اب½اذخت±£¬·ضDشعدك¶خACةد؛حةندكACةدء½ضضاé؟ِ£¬شظ·ض،دBDE£½90،م؛ح،دDBE£½90،م·ض±ً»ح¼£¬¸ù¾فب½اذخدàثئ؛حب½ا؛¯تءذ±بہت½؟ة½â¾ِختج⣮
£¨1£©شع،÷ABCضذ£¬
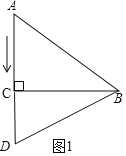
،ك،دACB=90،م£¬AB=5£¬![]() £¬
£¬
،à![]() £¬
£¬
،àBC=ABcos،دABC=5![]() 4£¬
4£¬
،à![]() £¬
£¬
µ±AD=AB=5ت±£¬،دABD=،دD£¬
،àCD=AD©پAC=5©پ3=2£¬
شعRt،÷BCDضذ£¬![]() £¬
£¬
،àtan،دABD=tan،دD=2£»
£¨2£©بçح¼2£¬،رA¾¹µمE£¬ء½ش²حâاذ£¬
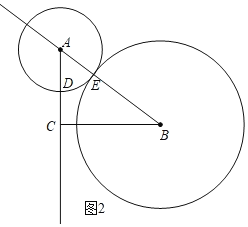
سةجâزâµأ£؛AD=t£¬BE=2t£¬
،àt+2t=5£¬
½âµأ£؛t![]() £¬
£¬
¢ظµ±ء½ش²حâہëت±£¬سةجâزâµأ5£¾3t£¬½âµأ£؛![]() £»
£»
¢عµ±ء½ش²حâاذت±£¬بçح¼2£¬![]() £»
£»
¢غµ±ء½ش²دཻت±£¬سةجâزâµأt£¼5£¼3t£¬½âµأ£؛![]() £»
£»
¢ـµ±ء½ش²ؤعاذت±£¬بçح¼3£¬سةجâزâµأ2t©پt=5£¬½âµأ£؛t=5£»
¢فµ±ء½ش²ؤع؛¬ت±£¬سةجâزâµأ0،ـ5£¼t£¬½âµأ£؛t£¾5£»
£¨3£©¢ظµ±Dشعدك¶خACةد£¬از،دBED=90،مت±£¬بçح¼4£¬
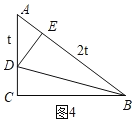
،كcosA![]() £¬¼´
£¬¼´![]() £¬
£¬
½âµأ£؛![]() £¬
£¬
،àCD=3![]() £¬
£¬
،à![]() £»
£»
¢عµ±Dشعدك¶خACةد£¬از،دBDE=90،م£¬بçح¼5£¬¹E×÷EF،خBC£¬½»ACسعF£¬
،àAE=5©پ2t£®
،كEF،خBC£¬
،à،÷AEF،×،÷ABC£¬
،à![]() £¬¼´
£¬¼´![]() £¬
£¬
،àAF=3![]() t£¬EF=4
t£¬EF=4![]() t£®
t£®
،كAD=t£¬
،àCD=3©پt£¬DF=AD©پAF=t©پ(3![]() t)
t)![]() t©پ3£®
t©پ3£®
،ك،دBDE=،دEDF+،دCDB=،دCDB+،دCBD=90،م£¬
،à،دEDF=،دCBD£®
،ك،دEFD=،دC=90،م£¬
،à،÷EFD،×،÷DCB£¬
،à![]() £¬¼´
£¬¼´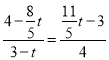 £¬
£¬
،à4(4![]() t)=(3©پt)(
t)=(3©پt)(![]() t©پ3)£¬
t©پ3)£¬
½âµأ£؛t1=5(ةل)£¬![]() £¬
£¬
،àtan،دCBD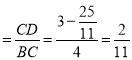 £»
£»
¢غµ±Dشعدك¶خACµؤرس³¤دكةد£¬از،دBDE=90،مت±£¬بçح¼6£¬¹E×÷EF،حAC£¬½»CAµؤرس³¤دكسعF£¬
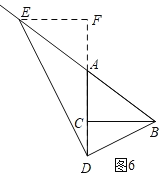
،كEF،خBC£¬
،à،÷AEF،×،÷ABC£¬
،à![]() £¬¼´
£¬¼´![]() £¬
£¬
،àAF![]() t©پ3£¬EF
t©پ3£¬EF![]() t©پ4£®
t©پ4£®
،كAD=t£¬
،àCD=t©پ3£¬DF=AD+AF=t+(![]() t©پ3)
t©پ3)![]() t©پ3£¬
t©پ3£¬
ح¬ہيµأ،÷EFD،×،÷DCB£¬
،à![]() £¬¼´
£¬¼´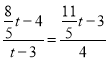 £¬
£¬
،à4(![]() t©پ4)=(t©پ3)(
t©پ4)=(t©پ3)(![]() t©پ3)£¬
t©پ3)£¬
½âµأ£؛t1=5£¬![]() (ةل)£¬
(ةل)£¬
،àtan،دCBD![]() £»
£»
¢ـµ±Dشعدك¶خACµؤرس³¤دكةد£¬از،دDBE=90،مت±£¬بçح¼7£¬
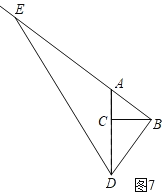
،ك،دABC+،دCBD=،دCBD+،دCDB£¬
،à،دABC=،دCDB£¬
،àtan،دABC=tan،دCDB![]() £¬¼´
£¬¼´![]() £¬
£¬
½âµأ£؛![]() £¬
£¬
،àtan،دCBD![]() £»
£»
×غةد£¬tan،دCBDµؤضµتا![]() »ٍ
»ٍ![]() »ٍ
»ٍ![]() »ٍ
»ٍ![]() £®
£®