��Ŀ����
����Ŀ��ij��ݹ�˾�мס�������������ͬһ·�ߴ�A�ص�B�����ͻ��ij������ͬʱ��A�س�����ʻ��B�أ�;���ҳ����ڳ��ֹ��ϣ�ͣ��������һ��ʱ�䣬������Ϻ��ҳ��ӿ����ٶ�����ʻ��B�أ��׳���A�ص�B���ٶ�ʼ�ձ��ֲ��䣮��ͼ��ʾ�Ǽס�������֮��ľ���y(km)����������ʱ��x(h)�ĺ���ͼ���������Ϣ����������⣺
(1)��M�������ʾ��ʵ��������ʲô��
(2)���MN����ʾ�Ĺ�ϵʽ����д���ҹ��Ϻ���ٶȣ�
(3)�����ǰ�������ٶ��Լ�a��ֵ��
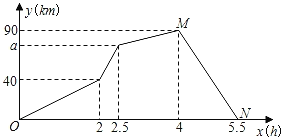
���𰸡�(1) ����ʻ4Сʱʱ���׳�����B��(�յ�)���ҳ������յ㻹��90ǧ�ף�(2) y=��60x+330��60ǧ��/Сʱ��(3) �׳��ٶ�Ϊ70ǧ��/Сʱ����Ϊ50ǧ��/Сʱ��a��ֵΪ75
��������
(1)�۲�ͼ������������ɵô𰸣�
(2)��MN����ʾ�Ĺ�ϵʽΪy=kx+b���ô���ϵ�������ý���ʽ������·�̳�����Ӧ��ʱ��ɵ��ٶȣ�
(3)�����ʱ���ٶ�Ϊvǧ��/Сʱ�����ٶ�Ϊ(v��20)ǧ��/Сʱ�������ҳ����ֹ��Ϻ��(2.5��2)Сʱ�׳���ʻ��·�̼����ҳ������ų�����������������ľ������90ǧ��ȥ40ǧ�ף��г�����v�ķ��̣����v��ֵ�����ҳ��ٶ�Ҳ����ã�Ȼ����40+70��0.5���㼴�ɵó�a��ֵ��
�⣺(1)�𣺵�M�������ʾ��ʵ�������ǣ�����ʻ4Сʱʱ���׳�����B��(�յ�)���ҳ������յ㻹��90ǧ�ף�
(2)��MN����ʾ�Ĺ�ϵʽΪy=kx+b����M(4��90)��N(5.5��0)����ã�
![]() ��
��
��ã�![]() ��
��
��MN����ʾ�Ĺ�ϵʽΪy=��60x+330��
�����ų����ҳ��ٶ�Ϊ��90��(5.5��4)=60ǧ��/Сʱ��
(3)��40��2=20ǧ��/Сʱ��
�������ʱ���ٶ�Ϊvǧ��/Сʱ�����ٶ�Ϊ(v��20)ǧ��/Сʱ�����У�
(2.5��2)v+(4��2.5)(v��60)=90��40��
��ã�v=70��
���׳��ٶ�Ϊ70ǧ��/Сʱ����Ϊ50ǧ��/Сʱ��
��a��ֵΪ40+70��0.5=75��