题目内容
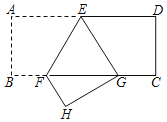
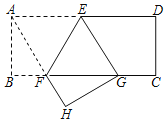
【题目】如图,矩形ABCD中,点E,F分别在AD,BC上,且AE=DE,BC=3BF,连接EF,将矩形ABCD沿EF折叠,点A恰好落在BC边上的点G处,则cos∠EGF的值为_____.
【答案】![]()
【解析】
连接AF,由矩形的性质得AD∥BC,AD=BC,由平行线的性质得∠AEF=∠GFE,由折叠的性质得∠AFE=∠GFE,AF=FG,推出∠AEF=∠AFE,则AF=AE,AE=FG,得出四边形AFGE是菱形,则AF∥EG,得出∠EGF=∠AFB,设BF=2x,则AD=BC=6x,AF=AE=FG=3x,在Rt△ABF中,cos∠AFB=![]() =
=![]() ,即可得出结果.
,即可得出结果.
解:连接AF,如图所示:
∵四边形ABCD为矩形,
∴AD∥BC,AD=BC,
∴∠AEF=∠GFE,
由折叠的性质可知:∠AFE=∠GFE,AF=FG,
∴∠AEF=∠AFE,
∴AF=AE,
∴AE=FG,
∴四边形AFGE是菱形,
∴AF∥EG,
∴∠EGF=∠AFB,
设BF=2x,则AD=BC=6x,AF=AE=FG=3x,
在Rt△ABF中,cos∠AFB=![]() =
=![]() =
=![]() ,
,
∴cos∠EGF=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目