题目内容
【题目】点O在直线PQ上,过点O作射线OC,使∠POC=130°,将一直角三角板的直角顶点放在点O处.
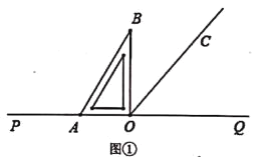
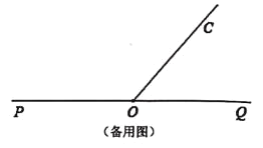
(1)如图①所示,将直角三角板AOB的一边OA与射线OP重合,则∠BOC=________°.
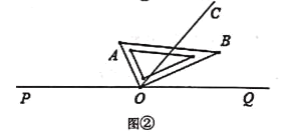
(2)将图①中的直角三角板AOB绕点O旋转一定角度得到如图②所示的位置,若OA平分∠POC,求∠BOQ的度数.
(3)将图①中的直角三角板AOB绕点O旋转一周,存在某一时刻恰有OB⊥OC,求出所有满足条件的∠AOQ的度数.
【答案】(1)40;(2)25°;(3)130°或50°
【解析】
(1))根据∠BOC=∠POC90°代入数据计算即可;
(2)2)根据角平分线的定义可得∠AOP=∠AOC= ![]() ∠POC=
∠POC= ![]() ×130°=65°,再由∠BOQ=180°-∠OP-∠AOB计算即可;
×130°=65°,再由∠BOQ=180°-∠OP-∠AOB计算即可;
(3)分当OB在∠POC内部时和当OB在∠POC外部时,计算即可.
解:(1)∵∠BOC=∠POC-∠AOB
∴∠BOC=130°-90°=40°.
故答案为:40°.
(2)解:∵OA平分∠POC,
∴∠AOP=∠AOC= ![]() ∠POC=
∠POC= ![]() ×130°=65°
×130°=65°
∴∠BOQ=180°-∠OP-∠AOB=180-65°-90°=25°
(3)解:如图1,当OB在∠POC内部时,则∠AOC=180°,
∴∠AOQ=∠POC=130
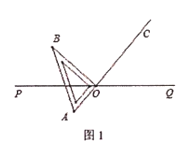
如图2,当OB在∠POC外部时,则OA与OC重合,

∴∠AOQ=∠COQ=180°-130°=50°
综上所述,∠AOQ的度数为130°或50°

【题目】如图,直线AB与y轴交于点A,与x轴交于点B,点A的纵坐标、点B的横坐标如图所示.
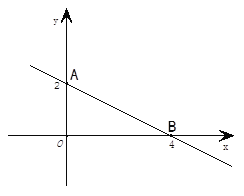
(1)求直线AB的解析式;
(2)点P在直线AB上,是否存在点P使得△AOP的面积为1,如果有请直接写出所有满足条件的点P的坐标
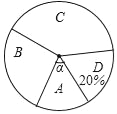
【题目】我市某中学举行演讲比赛,赛后整理参赛学生的成绩,将比赛成绩分为A,B,C,D四个等级,把结果列成下表(其中,m是常数)并绘制如图所示的扇形统计图(部分).
等级 | A | B | C | D |
人数 | 6 | 10 | m | 8 |
(1)求m的值和A等级所占圆心角α的大小;
(2)若从本次比赛中获得A等级的学生中,选出2名取参加市中心学生演讲比赛,已知A等级中男生有2名,求出所选2名学生中恰好是一名男生和一名女生的概率.