题目内容
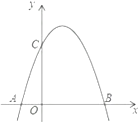
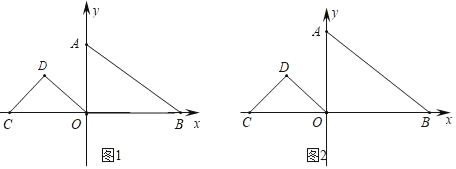
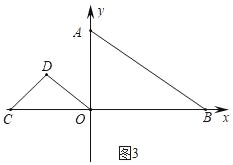
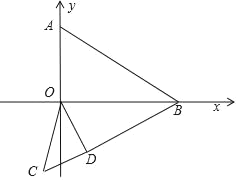
【题目】如图,已知在平面直角坐标系中,直线AB:![]() 与x轴、y轴分别交于B、A两点,等腰Rt△OCD,∠D=90°,C坐标为(﹣4,0).
与x轴、y轴分别交于B、A两点,等腰Rt△OCD,∠D=90°,C坐标为(﹣4,0).
(1)求A、B坐标;
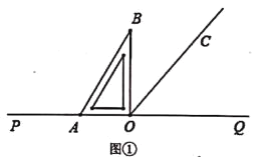
(2)将△OCD沿x轴正方形平移,速度为1个单位为每秒,时间为t(0≤t≤6),设△OCD与△OAB重叠面积为S,请写出S与t之间的函数关系式;
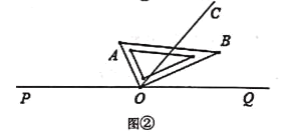
(3)将△OCD绕O点旋转,当O、B、D三点构成的三角形为直角三角形时,请直接写出D点坐标.
【答案】(1)![]() , B(6,0);(2)
, B(6,0);(2)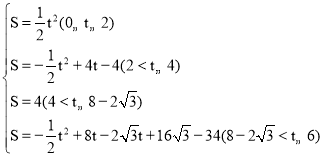 ;(3)点D的坐标为
;(3)点D的坐标为![]() ,
,![]() ,
,  ,
, 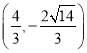 .
.
【解析】
1)分别令x=0,解得点A的坐标,令y=0,解得点B的坐标.
(2)分情况讨论,利用特殊角度求得线段之间存在的数量关系,再计算重叠部分面积.
(3)分情况讨论,O为直角顶点,D为直角顶点,再利用等面积法求得线段长度.
解:(1)令x=0,y=2![]() ,
,
∴A(0,2![]() ),
),
令y=0,即﹣![]() x+2
x+2![]() =0,
=0,
解得x=6,
∴B(6,0).
(2)∵C(﹣4,0),
∴OC=4,
∵△COD为等腰直角三角形,
∴CD=OD,设CD为a,则OD为a,
在Rt△OCD中,根据勾股定理得,a2+a2=42,
解得a=2![]() ,
,
①当0≤t≤2时,
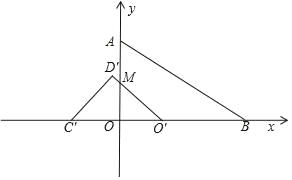
OO′=t,OM=t,
S=OO′OM![]() =
=![]() t2.
t2.
②2<t≤4时,

OO′=t,∴OC′=4﹣t,
∴OM=4﹣t,
S=![]() ×(2
×(2![]() )2﹣OC′OM
)2﹣OC′OM![]() =4﹣
=4﹣![]() (4﹣t)2=﹣
(4﹣t)2=﹣![]() t2+4t﹣4.
t2+4t﹣4.
③当4<t≤8﹣2![]() 时,
时,
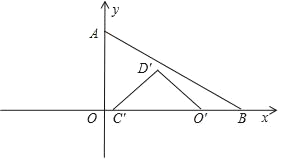
S=![]() ×(2
×(2![]() )2=4.
)2=4.
④8﹣2![]() <t≤6时,
<t≤6时,
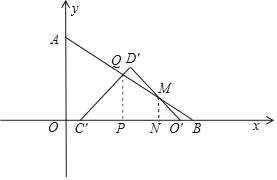
OO′=t,
∴BO′=6﹣t,
过M作MN垂直x轴,垂足为N,
设MN=NO′=x,
则BN=![]() x,
x,
∴![]() x﹣x=6﹣t,
x﹣x=6﹣t,
解得x=![]() ,
,
BC′=10﹣t,过点Q作x轴得垂线,垂足为P,
设PQ=PC′=y,则BP=![]() y,
y,
∴y+![]() y=10﹣t,
y=10﹣t,
解得y=![]() ,
,
∴S=BC′PQ![]() ﹣BO′MN
﹣BO′MN![]() =﹣
=﹣![]() t2+8t﹣2
t2+8t﹣2![]() t+16
t+16![]() ﹣34.
﹣34.
综上: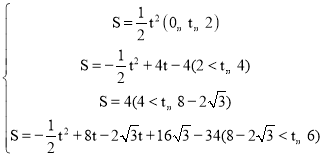
(3)①如图所示,

此时D(0,2![]() ).
).
②如图所示,
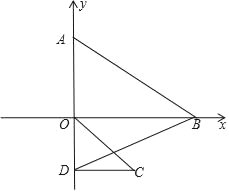
此时D(0,﹣2![]() ).
).
③如图所示,

此时∠BDO=90°,OD=2![]() ,OB=6,
,OB=6,
∴DB=2![]() ,
,
过D作DE垂直于x轴,垂足为点E,
ODDB![]() =OBDE
=OBDE![]() ,
,
解得DE=![]() ,
,
∴OE=![]() ,
,
∴D(![]() ,
,![]() ).
).
④如图所示,
此时的点D与③中的点D关于x轴对称,
∴D .
.
综上,点D的坐标为![]() ,
,![]() ,
, 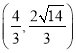 ,
,  .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案