Question

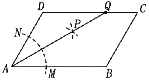
【题目】矩形纸片ABCD，AB=4，BC=12，E、F分别是AD、BC边上的点，ED=3．将矩形纸片沿EF折叠，使点C落在AD边上的点G处，点D落在点H处．

（1）矩形纸片ABCD的面积为

（2）如图1，连结EC，四边形CEGF是什么特殊四边形，为什么？

（3）M，N是AB边上的两个动点，且不与点A，B重合，MN=1，求四边形EFMN周长的最小值.（计算结果保留根号）

Answer 1

【答案】（1）48；（2）四边形CEGF是菱形，理由见详解；（3）四边形EFMN周长的最小值为.

【解析】

（1）矩形面积=长×宽，即可得到答案，

（2）利用对角线互相垂直平分的四边形是菱形进行证明，先证对角线相互垂直，再证对角线互相平分．

（3）明确何时四边形的周长最小，利用对称、勾股定理、三角形相似，分别求出各条边长即可．

解：（1）S矩形ABCD=ABBC=12×4=48，

故答案为：48．

（2）四边形CEGF是菱形，

证明：连接CG交EF于点O，

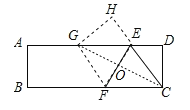
由折叠得：EF⊥CG，GO=CO，

∵ABCD是矩形，

∴AD∥BC，

∴∠OGE=∠OCF，∠GEO=∠CFO

∴△GOE≌△COF（AAS），

∴OE=OF

∴四边形CEGF是菱形．

因此，四边形CEGF是菱形．

（3）作F点关于点B的对称点F1，则NF1=NF，

当NF1∥EM时，四边形EFMN周长最小，

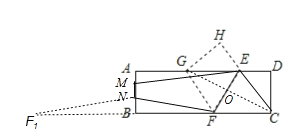
设EC=x，由（2）得：GE=GF=FC=x，

在Rt△CDE中，∵ED2+DC2=EC2，

∴32+42=EC2，

∴EC=5=GE=FC=GF，

在Rt△GCD中，，

∴OC=GO=，

在Rt△COE中，，

∴EF=2OE=，

当NF1∥EM时，易证△EAM∽△F1BN，

∴，

设AM=y，则BN=4-1-y=3-y，

∴，解得：，

此时，AM=，BN=，

由勾股定理得：

，

，

∴四边形EFMN的周长为：

故四边形EFMN周长的最小值为：.