题目内容
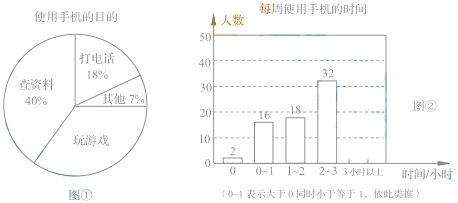
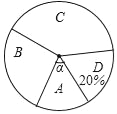
【题目】我市某中学举行演讲比赛,赛后整理参赛学生的成绩,将比赛成绩分为A,B,C,D四个等级,把结果列成下表(其中,m是常数)并绘制如图所示的扇形统计图(部分).
等级 | A | B | C | D |
人数 | 6 | 10 | m | 8 |
(1)求m的值和A等级所占圆心角α的大小;
(2)若从本次比赛中获得A等级的学生中,选出2名取参加市中心学生演讲比赛,已知A等级中男生有2名,求出所选2名学生中恰好是一名男生和一名女生的概率.
【答案】(1)m=16,A等级所占圆心角α=54°;(2)所选2名学生中恰好是一名男生和一名女生的概率为![]() .
.
【解析】分析:(1)先根据D等级人数及其百分比求得被调查的总人数,再用总人数减去A、B、D的人数求得m的值,用360°乘以A等级人数所占比例即可求出α的大小.
(2)设两位男生为a、b,四位女生为m、n、p、q,列出所有等可能结果,利用概率公式计算可得.
详解:(1)本次调查的总人数为8÷20%=40人,
则m=40﹣(6+10+8)=16,A等级所占圆心角α=360°×![]() =54°;
=54°;
(2)设两位男生为a、b,四位女生为m、n、p、q,
从6位同学中选取两人的所有等可能结果为:ab、am、an、ap、aq、bm、bn、bp、bq、mn、mp、mq、np、nq、pq共15种情况,
其中恰有1男1女的有8种结果,
所以所选2名学生中恰好是一名男生和一名女生的概率为![]() .
.

【题目】某市在今年对全市6000名八年级学生进行了一次视力抽样调查,并根据统计数据,制作了如图所示的统计表和统计图.
组别 | 视力 | 频数(人) |
|
| 20 |
|
|
|
|
|
|
|
| 70 |
|
| 10 |
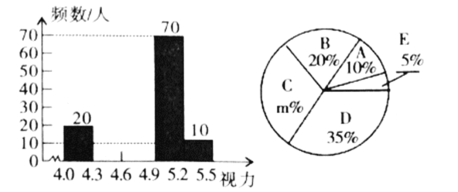
请根据图表信息回答下列问题:
(1)求抽样调查的人数;
(2)![]() ___________,
___________,![]() _____________,
_____________,![]() _____________;
_____________;
(3)补全频数分布直方图;
(4)若视力在4.9以上(含4.9)均属正常,则视力正常的人数占被统计人数的百分比是多少?