Question

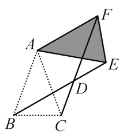
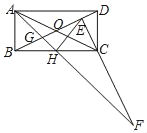
【题目】如图，矩形ABCD中，BC＝2AB，对角线相交与O点，过C点作CE⊥BD交BD于E点，H为BC中点，连接AH交BD于G点，交EC的延长线于F点，下列4个结论：①EH＝AB；②∠ABG＝∠HEC；③△ABG≌△HEC；④CF＝BD．正确的结论是（　　）

A.①②④B.①④C.③④D.①③④

Answer 1

【答案】A

【解析】

根据BC＝2AB，H为BC中点，可得△ABH为等腰直角三角形，HE＝BH＝HC，可得△CEH为等腰三角形，又∠BCD＝90°，CE⊥BD，利用互余关系得出角的相等关系，根据基本图形判断全等三角形，特殊三角形进行判断．

①在△BCE中，

∵CE⊥BD，H为BC中点，

∴BC＝2EH，又BC＝2AB，

∴EH＝AB，正确；

②由①可知，BH＝HE，

∴∠EBH＝∠BEH，

又∠ABG+∠EBH＝∠BEH+∠HEC＝90°，

∴∠ABG＝∠HEC，正确；

③由AB＝BH，∠ABH＝90°，得∠BAG＝45°，

同理：∠DHC＝45°，

∴∠EHC＞∠DHC＝45°，

∴△ABG≌△HEC，错误；

④∠ECH＝∠CHF+∠F＝45°+∠F，又∠ECH＝∠CDE＝∠BAO，∠BAO＝∠BAH+∠HAC，

∴∠F＝∠HAC，

∴CF＝BD，正确．

正确的有三个：①②④．

故选：A．