题目内容
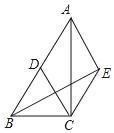
【题目】如图，在Rt△ABC中，∠ACB=90°，D为AB中点，AE∥CD，CE∥AB．
（1）试判断四边形ADCE的形状，并证明你的结论．
（2）连接BE，若∠BAC=30°，CE=1，求BE的长．
【答案】(1)见解析；（2）
【解析】试题分析： 
首先判定四边形ADCE是平行四边形，然后由直角三角形斜边上的中线的性质判定该平行四边形的邻边相等，即可证得四边形ADCE是菱形．
先求出
的度数，然后用勾股定理求解即可.
试题解析：（1）∵AE∥CD，CE∥AB，
∴四边形ADCE是平行四边形，
∵∠ACB=90°，D为AB的中点，
∴
∴四边形ADCE为菱形；
（2）∵∠BAC=30°，四边形ADCE为菱形，
∴
又∵
∴∠DBC=60°，而
∴
是等边三角形，
∴
∴
又∵
∴
∴
∴
中， 
又∵
∴
∴
练习册系列答案
相关题目
