Question

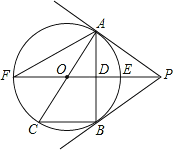
【题目】如图，已知在△ABC中，D，E，F分别是AB，BC，AC的中点，连结DF，EF，BF．

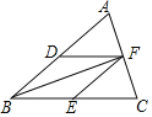
（1）求证：四边形BEFD是平行四边形；

（2）若∠AFB＝90°，AB＝4，求四边形BEFD的周长．

Answer 1

【答案】（1）见解析；（2）8

【解析】

（1）根据两组对边分别平行的四边形是平行四边形来证明即可；

（2）由∠AFB＝90°，得DF＝DB＝DA＝AB＝2，再根据菱形的判定定理求得四边形BEFD是菱形，进而求得答案．

（1）证明：∵D，E，F分别是AB，BC，AC的中点，

∴DF∥BC，EF∥AB，

∴四边形BEFD是平行四边形；

（2）解：∵∠AFB＝90°，D是AB的中点，AB＝4，

∴DF＝DB＝DA＝AB＝2，

∵四边形BEFD是平行四边形，

∴四边形BEFD是菱形，

∵DB＝2，

∴四边形BEFD的周长为：2×4=8．