题目内容
【题目】如图所示,AB是半圆O的直径,AC是弦,点P沿BA方向,从点B运动到点A,速度为1cm/s,若AB=10cm,点O到AC的距离为4cm.
(1)求弦AC的长;
(2)问经过多长时间后,△APC是等腰三角形.

【答案】(1)AC=6;(2)t=4或5或![]() s时,△APC是等腰三角形;
s时,△APC是等腰三角形;
【解析】
(1)过O作OD⊥AC于D,根据勾股定理求得AD的长,再利用垂径定理即可求得AC的长;(2)分AC=PC、AP=AC、AP=CP三种情况求t值即可.
(1)如图1,过O作OD⊥AC于D,
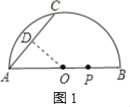
易知AO=5,OD=4,
从而AD=![]() =3,
=3,
∴AC=2AD=6;
(2)设经过t秒△APC是等腰三角形,则AP=10﹣t
①如图2,若AC=PC,过点C作CH⊥AB于H,
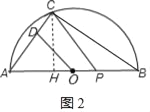
∵∠A=∠A,∠AHC=∠ODA=90°,
∴△AHC∽△ADO,
∴AC:AH=OA:AD,即AC:![]() =5:3,
=5:3,
解得t=![]() s,
s,
∴经过![]() s后△APC是等腰三角形;
s后△APC是等腰三角形;
②如图3,若AP=AC,
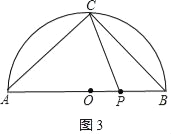
由PB=x,AB=10,得到AP=10﹣x,
又∵AC=6,
则10﹣t=6,解得t=4s,
∴经过4s后△APC是等腰三角形;
③如图4,若AP=CP,P与O重合,
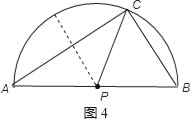
则AP=BP=5,
∴经过5s后△APC是等腰三角形.
综上可知当t=4或5或![]() s时,△APC是等腰三角形.
s时,△APC是等腰三角形.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目








