Question

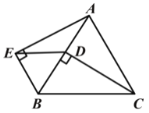
【题目】已知：平行四边形ABCD，求作菱形AECF，使点E、点F分别在BC、AD边上

下面是小明设计的尺规作图过程.

作法：如图

① 连接AC；

② 分别以A、C为圆心，大于AC的长为半径作弧，两弧交于M、N两点；

③ 连接MN，分别与BC、AD、AC交于E、F、O三点；

④ 连接AE、CF

四边形AECF即为所求

根据小明设计的尺规作图过程

（1）使用直尺和圆规，补全图形：（保留作图痕迹）

（2）完成下面的证明

证明∵AM= ，AN= ，

∴MN是AC的垂直平分线。

（ ）（填推理的依据）

∴EF⊥AC，OA=OC，

∴平行四边形ABCD

∴AD∥BC

∴∠FAO=∠ECO

在△FAO和△ECO中

∴△FAO≌△ECO

∴OE=OF

又∵OA=OC

∴四边形AECF是平行四边形

（ ）（填推理依据）

∵EF⊥AC

∴四边形AECF是菱形

（ ）（填推理依据）

Answer 1

【答案】（1）见解析；（2）见解析.

【解析】

（1）根据作法画出图形即可．

（2）先证明四边形AECF为平行四边形，然后利用对角线垂直的平行四边形为菱形得到结论．

解：（1）如图，四边形AECF为所求作的菱形．

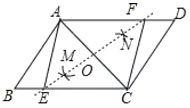
（2）证明：∵AM＝CM，AN＝CN，

∴MN是AC的垂直平分线，（到线段两端点的距离相等的点在线段的垂直平分线上）

∴EF⊥AC，OA＝OC

∵平行四边形ABCD

∴AD∥BC

∴∠FAO＝∠ECO，

在△FAO和△ECO中，，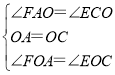

∴△FAO≌△ECO，

∴OE＝OF

又∵OA＝OC

∴四边形AECF是平行四边形，（对角线互相平分的四边形为平行四边形）

∵EF⊥AC，

∴四边形AECF是菱形．（对角线互相垂直的平行四边形为菱形）.

故答案为：CM，CN，到线段两端点的距离相等的点在线段的垂直平分线上；对角线互相平分的四边形为平行四边形；对角线互相垂直的平行四边形为菱形．