题目内容
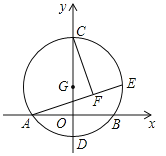
【题目】如图,以![]() 为圆心,半径为
为圆心,半径为![]() 的圆与
的圆与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 、
、![]() 两点,点
两点,点![]() 为⊙
为⊙![]() 上一动点,
上一动点,![]() 于
于![]() ,则弦
,则弦![]() 的长度为__________,当点
的长度为__________,当点![]() 在⊙
在⊙![]() 上运动的过程中,线段
上运动的过程中,线段![]() 的长度的最小值为__________.
的长度的最小值为__________.
【答案】 ![]() ;
; ![]()
【解析】作GM⊥AC于M,连接AG.因为∠AFC=90°,推出点F在以AC为直径的⊙M上,推出当点F在MG的延长线上时,FG的长最小,最小值=FM﹣GM,想办法求出FM、GM即可解决问题;
作GM⊥AC于M,连接AG.
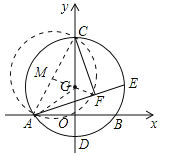
∵GO⊥AB,∴OA=OB.在Rt△AGO中,∵AG=2,OG=1,∴AG=2OG,OA=![]() =
=![]() ,∴∠GAO=30°,AB=2AO=2
,∴∠GAO=30°,AB=2AO=2![]() ,∴∠AGO=60°.
,∴∠AGO=60°.
∵GC=GA,∴∠GCA=∠GAC.
∵∠AGO=∠GCA+∠GAC,∴∠GCA=∠GAC=30°,∴AC=2OA=2![]() ,MG=
,MG=![]() CG=1.
CG=1.
∵∠AFC=90°,∴点F在以AC为直径的⊙M上,当点F在MG的延长线上时,FG的长最小,最小值=FM﹣GM=![]() ﹣1.
﹣1.
故答案为:2![]() ﹣1.
﹣1.

练习册系列答案
相关题目
【题目】西安市管理部门对“十一”国庆放假期间七天本市某景区客流变化量进行了不完全统计,数据如下(用正数表示客流量比前一天增加,用负数表示客流量比前一天下降):
日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
变化(万人) |
|
|
|
|
|
|
|
请通过计算解决以下问题:
(1)请判断这7天中,哪一天人数最多?哪一天人数最少?
(2)与10月3日相比,10月5日的客流量是上升了还是下降了?
(3)如图9月30日的客流量为1.5万人,据统计平均每人每天消费200元,请问该景区在“十一”七天国庆假期的总收入为多少万元?