Question

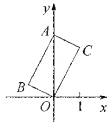
【题目】如图，在平面直角坐标系xOy中，四边形ABOC是矩形，点A在y轴上,若点C的坐标为(1,2)，则点B的坐标为________.

Answer 1

【答案】（1，）

【解析】

作CD⊥OA于D，BE⊥x轴于E，求出CD＝1，OD＝2，OC＝，证明△AOC∽△COD，得，求出OA＝，得出AD＝OAOD＝，证明△BOE≌△ACD（AAS），得出BE＝AD＝，OE＝CD＝1，即可得出答案．

解：作CD⊥OA于D，BE⊥x轴于E，如图所示：

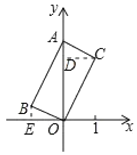
则∠CDA＝∠OEB＝90°，BE∥OA，

∴∠OBE＝∠AOB，

∵点C的坐标为（1，2），

∴CD＝1，OD＝2，

∴OC＝，

∵四边形ABOC是矩形，

∴OB＝AC，AC∥OB，∠ACO＝90°＝∠CDA，

∴∠AOB＝∠CAD，

∴∠OBE＝∠CAD，

∵∠AOC＝∠COD，

∴△AOC∽△COD，

∴，即，

∴OA＝，

∴AD＝OAOD＝，

在△BOE和△ACD中，，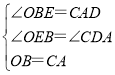

∴△BOE≌△ACD（AAS），

∴BE＝AD＝，OE＝CD＝1，

∴点B的坐标为（1，）；

故答案为：（1，）．