题目内容
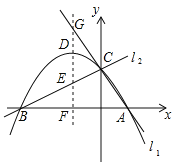
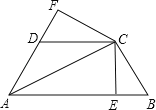
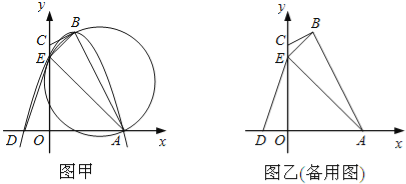
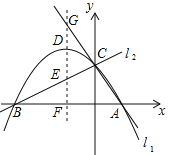
【题目】（2017四川省巴中市，第31题，12分）如图，已知两直线l1，l2分别经过点A（1，0），点B（﹣3，0），且两条直线相交于y轴的正半轴上的点C，当点C的坐标为（0，
）时，恰好有l1⊥l2，经过点A、B、C的抛物线的对称轴与l1、l2、x轴分别交于点G、E、F，D为抛物线的顶点．
（1）求抛物线的函数解析式；
（2）试说明DG与DE的数量关系？并说明理由；
（3）若直线l2绕点C旋转时，与抛物线的另一个交点为M，当△MCG为等腰三角形时，请直接写出点M的坐标．
【答案】（1）
；（2）DG=DE；（3）（﹣2，
），（﹣1，
）．
【解析】试题（1）设抛物线的函数解析式为
．将点A、B、C的坐标代入，得到关于a、b、c的方程组，解方程求出a、b、c的值，进而得到抛物线的解析式；
（2）利用待定系数法分别求出直线l1、直线l2的解析式，再求出G、D、E的坐标，计算得出DG的长；
（3）当△MCG为等腰三角形时，分三种情况：①GM=GC；②CM=CG；③MC=MG．
试题解析：解：（1）设抛物线的函数解析式为．
∵点A（1，0），点B（﹣3，0），点C（0，）在抛物线上，∴
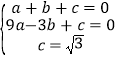，解得：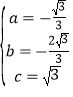
，∴抛物线的函数解析式为；
（2）DG=DE．理由如下：
设直线l1的解析式为y=k1x+b1，将A（1，0），C（0，）代入，解得
；
设直线l2的解析式为y=k2x+b2，将B（﹣3，0），C（0，）代入，解得
；
∵抛物线与x轴的交点为A（1，0），B（﹣3，0），∴抛物线的对称轴为直线x=﹣1，又∵点G、D、E均在对称轴上，∴G（﹣1，
），D（﹣1，），E（﹣1，
），∴DG=﹣=，DE=﹣=，∴DG=DE；
（3）若直线l2绕点C旋转时，与抛物线的另一个交点为M，当△MCG为等腰三角形时，分三种情况：
①以G为圆心，GC为半径画弧交抛物线于点M1、C，点M1与C关于抛物线的对称轴对称，则M1的坐标为（﹣2，）；
②以C为圆心，GC为半径画弧交抛物线于点M2、M3，点M2与点A重合，点A、C、G在一条直线上，不能构成三角形，M3与M1重合；
③作线段GC的垂直平分线，交抛物线于点M4、M5，点M4与点D重合，点D的坐标为（﹣1，），M5与M1重合；
综上所述：满足条件的点M只有两个，其坐标分别为（﹣2，），（﹣1，）．
