��Ŀ����
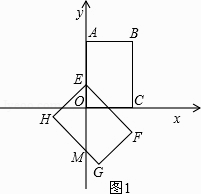
����Ŀ����ͼ������OABC��ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��A��0��4����C��2��0����������OABC�Ƶ�O��˳ʱ�뷽����ת135�㣬�õ�����EFGH����E��O�غϣ���
��1����GH��y���ڵ�M�����FOM=�㣬OM=��
��2��������EFGH��y������ƽ��t����λ��
��ֱ��GH��x�ύ�ڵ�D����AD��BO����t��ֵ��
��������EFGH�����OABC�ص����ֵ����ΪS��ƽ����λ������0��t��4 ![]() ��2ʱ��S��t֮��ĺ�����ϵʽ��
��2ʱ��S��t֮��ĺ�����ϵʽ��
���𰸡�
��1��45�㣻2 ![]()
��2��
�⣺����ͼ��ʾ������AD��BO

��AD��BO��AB��OD��
���ı���ADOBΪƽ���ı��Σ�
��DO=AB=2��
��ƽ�ƿ�֪����HEM=45�㣬
���OMD=��ODM=45�㣬
��OM=OD=2��
��ƽ�ƿ�֪��EM=2 ![]() ��
��
�����EFGHƽ�Ƶ�·��t=2 ![]() ��2=2��
��2=2�� ![]() ��1����
��1����
�ڷ�����������ǣ�
��i����ͼ1��ʾ����0��t��2ʱ���ص�����Ϊ����ֱ�������Σ�
��ʱOE=t�����ص��������S= ![]() t2��
t2��
��ii����ͼ2��ʾ����2��t��2 ![]() ʱ���ص�����Ϊֱ�����Σ�
ʱ���ص�����Ϊֱ�����Σ�
��ʱS= ![]() [��t��2��+t]��2=2t��2��
[��t��2��+t]��2=2t��2��

��iii����ͼ3��ʾ����2 ![]() ��t��4
��t��4 ![]() ��2ʱ��E����A���·����ص�����Ϊ����Σ�
��2ʱ��E����A���·����ص�����Ϊ����Σ�
��ʱS=��2t��2���� ![]() ��t��2
��t��2 ![]() ��2=��
��2=�� ![]() t2+2��
t2+2�� ![]() +1��t��6��
+1��t��6��

���ϣ�S=  ��
��
���������⣺��1����ͼ��ʾ��
����ת�ɵã���AOF=135�㣬�֡�AOC=90�㣬
���COF=��AOF����AOC=45�㣬�֡�MOC=90�㣬
���FOM=45�㣬��OF��HG��
���OMH=��FOM=45�㣬�֡�H=90�㣬
���OHMΪ����ֱ�������Σ�
��OH=HM=2��
����ݹ��ɶ����ã�OM=2 ![]() ��
��
�����㾫����������Ĺؼ���������ɶ����ĸ�������֪ʶ������ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2���Լ������εĶ�������⣬�˽�һ��Ա�ƽ�У���һ��Ա߲�ƽ�е��ı��������Σ�������ȵ������ǵ������Σ�








