题目内容
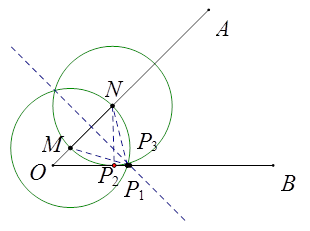
【题目】如图,∠AOB=45°,点M,N在边OA上,OM=x,ON=x+4,点P是边OB上的点.若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是.
【答案】x=0或x= ![]() 或4≤x<4
或4≤x<4 ![]()
【解析】解:以MN为底边时,可作MN的垂直平分线,与OB必有一个交点P1 , 且MN=4,以M为圆心MN为半径画圆,以N为圆心MN为半径画圆,
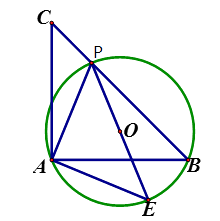
①如下图,当M与点O重合时,即x=0时,
除了P1 , 当MN=MP,即为P3;当NP=MN时,即为P2;
只有3个点P;
②当0<x<4时,如下图,圆N与OB相切时,NP2=MN=4,且NP2⊥OB,此时MP3=4,
则OM=ON-MN= ![]() NP2-4=
NP2-4= ![]() .
.
③因为MN=4,所以当x>0时,MN<ON,则MN=NP不存在,
除了P1外,当MP=MN=4时,
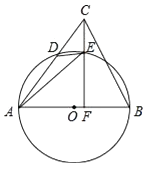
过点M作MD⊥OB于D,当OM=MP=4时,圆M与OB刚好交OB两点P2和P3;
当MD=MN=4时,圆M与OB只有一个交点,此时OM= ![]() MD=4
MD=4 ![]() ,
,
故4≤x<4 ![]() .
.
与OB有两个交点P2和P3 ,
所以答案是x=0或x= ![]() 或4≤x<4
或4≤x<4 ![]() .
.
【考点精析】掌握相交两圆的性质是解答本题的根本,需要知道相交的两个圆的连心线垂直平分两圆的公共弦.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目