题目内容
【题目】如图,已知矩形ABCD中,F是BC上一点,且AF=BC,DE⊥AF,垂足是E,连接DF.求证: 
(1)△ABF≌△DEA;
(2)DF是∠EDC的平分线.
【答案】
(1)证明:∵四边形ABCD是矩形,
∴∠B=90°,AD=BC,AD∥BC,
∴∠DAE=∠AFB,
∵DE⊥AF,
∴∠DEA=∠B=90°,
∵AF=BC,
∴AF=AD,
在△DEA和△ABF中
∵ 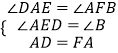 ,
,
∴△DEA≌△ABF(AAS)
(2)证明:∵由(1)知△ABF≌△DEA,
∴DE=AB,
∵四边形ABCD是矩形,
∴∠C=90°,DC=AB,
∴DC=DE.
∵∠C=∠DEF=90°
∴在Rt△DEF和Rt△DCF中
![]()
∴Rt△DEF≌Rt△DCF(HL)
∴∠EDF=∠CDF,
∴DF是∠EDC的平分线
【解析】(1)根据矩形性质得出∠B=90°,AD=BC,AD∥BC,推出∠DAE=∠AFB,求出AF=AD,根据AAS证出即可;(2)有全等推出DE=AB=DC,根据HL证△DEF≌△DCF,根据全等三角形的性质推出即可.
【考点精析】解答此题的关键在于理解角平分线的性质定理的相关知识,掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上,以及对矩形的性质的理解,了解矩形的四个角都是直角,矩形的对角线相等.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目