题目内容
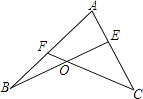
【题目】如图,△ABC中,D、E在AB上,且D、E分别是AC、BC的垂直平分线上一点.
(1)若△CDE的周长为4,求AB的长;
(2)若∠ACB=100°,求∠DCE的度数;
(3)若∠ACB=a(90°<a<180°),则∠DCE=。
【答案】
(1)解:∵D、E分别是AC、BC的垂直平分线上一点,∴DC=DA,EC=EB,
∵△CDE的周长=DC+DE+EC=4,
∴DA+DE+EB=4,即AB的长为4
(2)解:∵∠ACB=100°,∴∠A+∠B=80°,
∵DC=DA,∴∠DCA=∠A,
∵EC=EB,∴∠ECB=∠B,
∴∠DCA+∠ECB=80°,
∴∠DCE=100°-80°=20°
(3)2α-180°
【解析】(3)∵∠ACB=α,∴∠A+∠B=180°-α,
∵DC=DA,∴∠DCA=∠A,
∵EC=EB,∴∠ECB=∠B,
∴∠DCA+∠ECB=180°-α,
∴∠DCE=α-180°+α=2α-180°,
故答案为:2α-180°。
(1)根据线段垂直平分线上的点与线段的两个端点的距离相等,求出AB的长;(2)根据三角形内角和定理和等边对等角,求出∠DCE的度数;(3)根据三角形内角和定理和等边对等角,求出∠DCE的代数式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目