题目内容
【题目】已知:如图,点E在AC上,点F在AB上,BE,CF交于点O,且∠C=2∠B,∠BFC比∠BEC大20°,求∠C的度数. 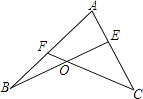
【答案】解:由三角形的外角性质,∠BFC=∠A+∠C,∠BEC=∠A+∠B, ∵∠BFC比∠BEC大20°,
∴(∠A+∠C)﹣(∠A+∠B)=20°,
即∠C﹣∠B=20°,
∵∠C=2∠B,
∴∠B=20°,∠C=40°
【解析】根据三角形的一个外角等于与它不相邻的两个内角的和列式表示出∠BFC和∠BEC,然后列出方程求出∠C、∠B即可.
【考点精析】解答此题的关键在于理解三角形的外角的相关知识,掌握三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


