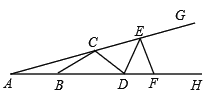
题目内容
【题目】在![]() 中,
中,![]() ,以
,以![]() 为边作等腰直角
为边作等腰直角![]() ,使
,使![]() ,边
,边![]() 交
交![]() 于点
于点![]() .
.
(1)如图1,过点![]() 作
作![]() 于点
于点![]() ,当
,当![]() 时,求线段
时,求线段![]() 的长;
的长;
(2)如图2,过点![]() 作
作![]() 于点
于点![]() ,且
,且![]() ,连接
,连接![]() , 若
, 若![]() 为
为![]() 的中点,求证:
的中点,求证:![]() .
.

【答案】(1)![]() +1;(2)见解析;
+1;(2)见解析;
【解析】
(1)利用等腰直角![]() 求出BD=2
求出BD=2![]() ,∠ABD=45
,∠ABD=45![]() 得到AH=
得到AH=![]() ,∠HAD=45
,∠HAD=45![]() ,再由
,再由![]() ,
, ![]() 得到EC=BE,∠EAH=
得到EC=BE,∠EAH=![]() ,利用勾股定理求出HE,即可得到EC的长;
,利用勾股定理求出HE,即可得到EC的长;
(2)连接CD,利用SAS证明△ABF≌△DAC,得到AF=CD. 过点C作CH⊥AB,交BD于G,连接AG,通过证明△CGE≌△ADE证得四边形ADCG是平行四边形,得到AG=CD,
再根据![]() 得到AG=DG=BG,得到AF=CD=DG=2DE.
得到AG=DG=BG,得到AF=CD=DG=2DE.
(1)∵等腰直角![]() ,
,![]() ,
,![]() ,
,
∴∠ABD=45![]() ,AB=
,AB=![]() ,
,
∴BD=![]() ,
,
∵![]() ,
,
∴AH=![]() ,∠HAD=45
,∠HAD=45![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() ,∠DAC=15
,∠DAC=15![]() ,
,
∴![]() ,
,![]() ,∠EAH=
,∠EAH=![]() ,
,
∴∠C=∠EBC,
∴EC=BE
设HE=x,则AE=2x,
∵![]() ,
,
∴![]() ,
,
得x=1,∴HE=1,
∴EC=BE=BH+HE=![]() +1.
+1.
(2)连接CD,
∵AC=BC,
∴∠ABC=∠BAC,
∵![]() ,
,
∴∠FBC=![]() ,
,
∴∠FBA=∠CAD,
∵![]() 是等腰直角三角形,
是等腰直角三角形,
∴AB=AD,
∵AC=BC=FB,
∴△ABF≌△DAC,
∴AF=CD,
过点C作CH⊥AB,交BD于G,连接AG,
∴CH∥AD,
∴∠ACH=∠DAC,
∵∠CEG=∠AED,AE=CE,
∴△CGE≌△ADE,
∴CG=AD,GE=DE
∴四边形ADCG是平行四边形,
∴AG=CD,
∵AC=BC, CH⊥AB,
∴AH=BH,
∵CH∥AD,
∴![]() ,
,
∴BG=GD,
∴AG=BG=DG,
∴AG=2DE,
∴AF=CD=AG=2DE.


练习册系列答案
相关题目