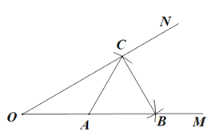
题目内容
【题目】如图,![]() 内接于
内接于![]() ,
,![]() ,
,![]() 是
是![]() 的直径,点
的直径,点![]() 是
是![]() 延长线上一点,且
延长线上一点,且![]() .
.

![]() 求证:
求证:![]() 是
是![]() 的切线;
的切线;
![]() 若
若![]() ,求
,求![]() 的直径.
的直径.
【答案】(1)详见解析;(2)![]() 的直径为
的直径为![]() .
.
【解析】
(1)连接OA,根据圆周角定理首先求得∠AOC的度数,然后根据三角形内角和定理求得∠OAP=90°,从而求解;
(2)根据直角三角形的性质,直角三角形中30°所对的边等于斜边的一半,即可求解.
(1)连接OA.
∵∠B=60°,∴∠AOC=2∠B=120°,∠AOD=180°-120°=60°.
又∵OA=OC,∴∠OAC=∠OCA=30°.
又∵AP=AC,∴∠P=∠ACP=30°,∴∠OAP=180°-∠AOD﹣∠P=90°,∴OA⊥PA,∴PA是⊙O的切线.
(2)设该圆的半径为x.
在Rt△OAP中,∵∠P=30°,∴PO=2OA=OD+PD.
又∵OA=OD,∴1+x=2x,解得:x=1,∴OA=PD=1,所以⊙O的直径为2.

练习册系列答案
相关题目