题目内容
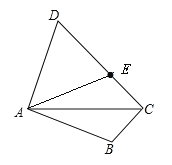
【题目】如图,![]() ,点B关于
,点B关于![]() 的对称点E恰好落在
的对称点E恰好落在![]() 上,若
上,若![]() ,则
,则![]() 的度数为( )
的度数为( )
A.45°B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
连接BE.由轴对称的性质得到AC垂直平分BE,进而得到∠BAC=∠EAC,∠BCA=∠ECA.根据等腰三角形的性质得到∠D=∠AED.设∠EAC=y,∠ACB=x,则∠BAC=y,∠ACE=x.然后根据三角形外角的性质和三角形内角和定理可得α+2x=180°,即可得到结论.
如图,连接BE.
∵点B关于AC的对称点E恰好落在CD上,
∴AC垂直平分BE,
∴AB=AE,BC=EC,
∴∠BAC=∠EAC,∠BCA=∠ECA.
∵AB=AD,∴AD=AE,∴∠D=∠AED.
设∠EAC=y,∠ACB=x,则∠BAC=y,∠ACE=x.
∴∠DAE=∠DAB-∠EAC-∠BAC=![]() .
.
∵∠AED=∠EAC+ECA=x+y,∴∠D=x+y.
∵∠DAE+∠AED+∠D=180°,∴![]() +x+y+x+y=180°,
+x+y+x+y=180°,
∴![]() =180°,
=180°,
∴x=![]() (180°-α)=90°
(180°-α)=90°![]() .
.
即∠ACB=90°![]() .
.
故选D.


【题目】某企业为杭州计算机产业基地提供电脑配件.受美元走低的影响,从去年1至9月,该配件的原材料价格一路攀升,每件配件的原材料价格y1(元)与月份x(1≤x≤9,且x取整数)之间的函数关系如下表:
月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
价格y1(元/件) | 560 | 580 | 600 | 620 | 640 | 660 | 680 | 700 | 720 |
随着国家调控措施的出台,原材料价格的涨势趋缓,10至12月每件配件的原材料价格y2(元)与月份x(10≤x≤12,且x取整数)之间存在如图所示的变化趋势:
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出y1 与x之间的函数关系式,根据如图所示的变化趋势,直接写出y2与x之间满足的一次函数关系式;
(2)若去年该配件每件的售价为1000元,生产每件配件的人力成本为50元,其它成本30元,该配件在1至9月的销售量p1(万件)与月份x满足关系式p1=0.1x+1.1(1≤x≤9,且x取整数),10至12月的销售量p2(万件)p2=﹣0.1x+2.9(10≤x≤12,且x取整数).求去年哪个月销售该配件的利润最大,并求出这个最大利润.