题目内容
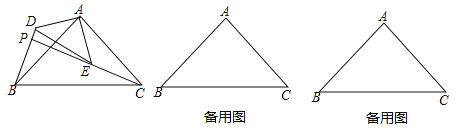
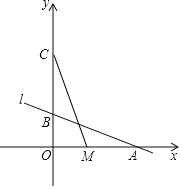
【题目】成都市天府一南站城市立交桥是成都市政府确定的城建标志性建筑,如图是立交桥引申出的部分平面图,测得拉索AB与水平桥面的夹角是37°,拉索DE与水平桥面的夹角是67°,两拉索顶端的距离AD为2m,两拉索底端距离BE为10m,请求出立柱AC的长.(参考数据tan37°≈![]() ,sin37°≈
,sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan67°≈
,tan67°≈![]() ,sin67°≈
,sin67°≈![]() ,cos67°≈
,cos67°≈![]() )
)

【答案】立柱AC的长为10m.
【解析】
设CE=xm,则BC=(10+x)m,解直角三角形即可得到结论.
解:设CE=xm,则BC=(10+x)m,
在Rt△CDE中,∵∠DEC=67°,
∴CD=CEtan67°=![]() x,
x,
在Rt△ABC中,∵∠B=37°,
∴AC=BCtan37°=![]() ×(10+x),
×(10+x),
∴AD=AC﹣CD=![]() ×(10+x)﹣
×(10+x)﹣![]() x=2,
x=2,
解得:x=![]() ,
,
∴AC=AD+CD=2+![]() ×
×![]() =10(m),
=10(m),
答:立柱AC的长为10m.

 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案【题目】某初中学校餐厅为了解学生对早餐的要求,随即抽样调查了该校的部分学生,并根据其中两个单选问题的调查结果,绘制了如下尚不完整的统计图表.
学生能接受的早餐价格统计表
价格分组(单位:元) | 频数 | 频率 |
0<x≤2 | 60 | 0.15 |
2<x≤4 | 180 | c |
4<x≤6 | 92 | 0.23 |
6<x≤8 | a | 0.12 |
x>8 | 20 | 0.05 |
合计 | b | 1 |
根据以上信息解答下列问题:
(1)统计表中,a= ,b= ,c= .
(2)扇形统计图中,m的值为 ,“甜”所对应的圆心角的度数是 .
(3)该餐厅计划每天提供早餐2000份,其中咸味大约准备多少份较好?

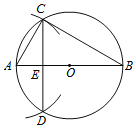
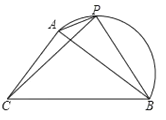
【题目】如图,在△ABC中,AB=4cm.BC=5cm,P是![]() 上的动点.设A,P两点间的距离为xcm,
上的动点.设A,P两点间的距离为xcm,
B,P两点间的距离为![]() cm,C,P两点间的距离为
cm,C,P两点间的距离为![]() cm.
cm.
小腾根据学习函数的经验,分别对函数![]() ,
,![]() 随自变量x的变化而变化的规律进行了探究.
随自变量x的变化而变化的规律进行了探究.
下面是小腾的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了![]() ,
,![]() 的几组对应值:
的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 |
| 4.00 | 3.69 | 2.13 | 0 | |
| 3.00 | 3.91 | 4.71 | 5.23 | 5 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,![]() ),(x,
),(x,![]() ),并画出函数
),并画出函数![]() ,
,![]() 的图象:
的图象:
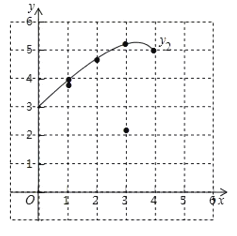
(3)结合函数图象.
①当△PBC为等腰三角形时,AP的长度约为____cm.
②记![]() 所在圆的圆心为点O,当直线PC恰好经过点O时,PC的长度约为_____cm.
所在圆的圆心为点O,当直线PC恰好经过点O时,PC的长度约为_____cm.