题目内容
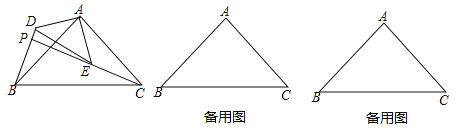
【题目】如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.
(1)求证:BD=CE;
(2)若AB=2,AD=1,把△ADE绕点A旋转,当∠EAC=90°时,求PB的长;
【答案】(1)证明见解析;(2)PB的长为![]() 或
或![]() .
.
【解析】试题分析:(1)依据等腰三角形的性质得到AB=AC,AD=AE,依据同角的余角相等得到∠DAB=∠CAE,然后依据SAS可证明△ADB≌△AEC,最后,依据全等三角形的性质可得到BD=CE;
(2)分为点E在AB上和点E在AB的延长线上两种情况画出图形,然后再证明△PEB∽△AEC,最后依据相似三角形的性质进行证明即可.
试题解析:解:(1)∵△ABC和△ADE是等腰直角三角形,∠BAC=∠DAE=90°,∴AB=AC,AD=AE,∠DAB=∠CAE,∴△ADB≌△AEC,∴BD=CE.
(2)解:①当点E在AB上时,BE=AB﹣AE=1.
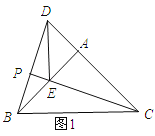
∵∠EAC=90°,∴CE=![]() =
=![]() .
.
同(1)可证△ADB≌△AEC,∴∠DBA=∠ECA.
∵∠PEB=∠AEC,∴△PEB∽△AEC,∴![]() ,∴
,∴![]() ,∴PB=
,∴PB=![]() .
.
②当点E在BA延长线上时,BE=3.
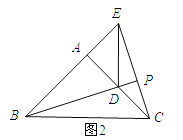
∵∠EAC=90°,∴CE=![]() =
=![]() .
.
同(1)可证△ADB≌△AEC,∴∠DBA=∠ECA.
∵∠BEP=∠CEA,∴△PEB∽△AEC,∴![]() ,∴
,∴![]() ,∴PB=
,∴PB=![]() .
.
综上所述,PB的长为![]() 或
或![]() .
.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案【题目】某校七年级组织数学嘉年华活动,共评出三个奖项,年级处购买了一些奖品进行表彰,相关统计结果如下表(不完整)所示:
一等奖 | 二等奖 | 三等奖 | 合计 | |
获奖人数(单位:人) | 40 | |||
奖品单价(单位:元) | 12 | 9 | 6 | |
奖品金额(单位:元) | 300 |
已知二等奖的获奖人数比一等奖的获奖人数多5人.你能根据所给条件,分别求出三种奖项的获奖人数吗?请根据你所设的未知数,先填表(代数式不必化简),再列方程解答.