Question

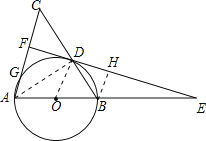
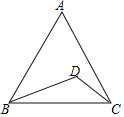
【题目】（白云区校级二模）如图，在△ABC中，AB＝10，BC＝12，以AB为直径的⊙O交BC于点D.过点D的⊙O的切线垂直AC于点F，交AB的延长线于点E.

（1）连接OD，则OD与AC的位置关系是　 　.

（2）求AC的长.

（3）求sinE的值.

Answer 1

【答案】（1）平行；（2）10；（3）

【解析】

（1）连接OD，由EF为圆O的切线，利用切线的性质得到OD⊥EF，再由AF⊥EF，可得OD∥AC；

（2）根据O为AB的中点，且OD与AF平行，得到OD为三角形ABC的中位线，得到OD为AC的一半，由OD的长求出AC的长即可；

（3）由（2）得到D为BC中点，求出BD与DC长，过B点作EF的垂线BH，垂足为H点，连接AD，可得BH，OD，AC三直线平行，由AB为圆O的直径，利用直径所对的圆周角为直角，得到∠ADB＝90°，再利用弦切角等于夹弧所对的圆周角，得到三角形DBH与三角形ABD相似，由相似得比例求出BH的长，再由BH与OD平行得到三角形BHE与三角形ODE相似，由相似得比例求出BE的长，在直角三角形BHE中，利用锐角三角函数定义求出sinE的值即可．

（1）连接OD，则OD与AC的位置关系是平行，

理由：∵EF与圆O相切，

∴OD⊥EF，

∵AF⊥EF，

∴OD∥AC；

故答案为：平行；

（2）∵O为AB中点，OD∥AC，且OD＝AO＝OB＝5，

∴OD为△BAC的中位线，

∴ODAC，

∴AC＝2OD＝10；

（3）由（2）知D为BC的中点，

∴BD＝CD＝6，

过B点作EF的垂线BH，垂足为H点，连接AD，

则有BH∥OD∥AC，

∵AB是直径，

∴∠ADB＝90°，

∵∠HDB＝∠DAB，∠ADB＝∠DHB＝90°，

∴△DBH∽△ABD，

∴，即，

解得：BH＝，

设BE＝x，

∵BH∥OD，

∴△EHB∽△EDO，

∴，即，

解得：x，即BE，

∴sinE．
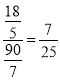