题目内容
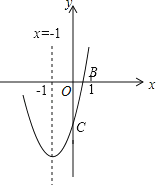
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx﹣3a(a≠0)经过点A(﹣1,0).
(1)求抛物线的顶点坐标;(用含a的式子表示)
(2)已知点B(3,4),将点B向左平移3个单位长度,得到点C.若抛物线与线段BC恰有一个公共点,结合函数的图象,求a的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)根据抛物线![]() 经过点
经过点![]() 可得a和b的关系,然后将抛物线解析式化为顶点式,即可得到该抛物线的顶点坐标;
可得a和b的关系,然后将抛物线解析式化为顶点式,即可得到该抛物线的顶点坐标;
(2)先根据点坐标平移的变化规律可得点C的坐标,画出当![]() 和
和![]() 时抛物线的图象,然后结合图象即可得到a的取值范围.
时抛物线的图象,然后结合图象即可得到a的取值范围.
(1)∵点![]() 在抛物线
在抛物线![]() 上
上
∴![]() ,解得
,解得![]()
∴![]()
∴抛物线的顶点坐标为![]() ;
;
(2)∵![]()
∴抛物线与x轴的另一个交点坐标为点![]() ,与y轴交于点
,与y轴交于点![]()
∵将点![]() 向左平移3个单位长度
向左平移3个单位长度
![]() 点C的坐标为
点C的坐标为![]() ,即
,即![]()
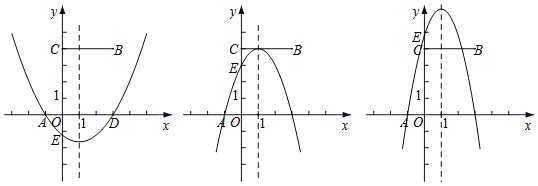
由题意,分以下两种情况:
①如图,当![]() 时
时
由抛物线与x、y轴的交点可知,抛物线与线段BC无公共点
②当![]() 时
时
若抛物线的顶点在线段BC上,则顶点坐标为![]()
∴![]()
解得![]()
若抛物线的顶点不在线段BC上,要使抛物线与线段BC恰有一个公共点,则抛物线与y轴的交点位于点C的上方
即![]()
解得![]()
综上,a的取值范围是![]() 或
或![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目